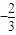题目内容
设sinα=sinθ+cosθ,sin2β=2sinθ•cosθ,则( )
分析:将sinα=sinθ+cosθ两边平方,由平方关系化简后,再把sin2β代入即可.
解答:解:∵sinα=sinθ+cosθ,sin2β=2sinθ•cosθ
∴sin2α=sin2θ+cos2θ+2sinθ•cosθ,
∴sin2α=1+sin2β,
故选A.
∴sin2α=sin2θ+cos2θ+2sinθ•cosθ,
∴sin2α=1+sin2β,
故选A.
点评:本题考查了同角三角函数关系:平方关系的应用,属于基础题.

练习册系列答案
相关题目
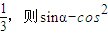 β,的最大值为( )
β,的最大值为( )