题目内容
10．设实数x，y满足约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$，则目标函数z=x-3y的最大值为（ ）| A． | 7 | B． | -$\frac{1}{3}$ | C． | -26 | D． | 6 |
分析 作出可行域，变形目标函数，平移直线y=$\frac{1}{3}$x结合图象可得．
解答 
解：作出约束条件$\left\{\begin{array}{l}{2x+y≤4}\\{x-y≤1}\\{x+2≥0}\end{array}\right.$所对应的可行域（如图阴影），
变形目标函数可得y=$\frac{1}{3}$x-$\frac{1}{3}$z，平移直线y=$\frac{1}{3}$x可知，
当直线经过点A（-2，-3）时，直线的截距最小值，
此时目标函数取最大值z=-2-3（-3）=7，
故选：A．
点评 本题考查简单线性规划，准确作图是解决问题的关键，属中档题．
练习册系列答案
相关题目
20．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：
（1）求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$，并在坐标系中画出
回归直线；
（2）试预测加工10个零件需要多少小时？
（注：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$，$\hat a=\bar y-\hat b\bar x$，$\sum_{i=1}^4{{x_i}{y_i}=52.5}$，$\sum_{i=1}^4{{x_i}^2}=54$）
| 零件的个数 x（个） | 2 | 3 | 4 | 5 |
| 加工的时间 y（小时） | 2.5 | 3 | 4 | 4.5 |
回归直线；
（2）试预测加工10个零件需要多少小时？
（注：$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\bar x}^2}}}}$，$\hat a=\bar y-\hat b\bar x$，$\sum_{i=1}^4{{x_i}{y_i}=52.5}$，$\sum_{i=1}^4{{x_i}^2}=54$）
18．已知k∈R，直线l1：kx+y=0过定点P，直线l2：kx-y-2k+2=0过定点Q，若动点M在以PQ为直径的圆上，则|MP|+|MQ|的最大值是（ ）
| A． | 2$\sqrt{2}$ | B． | 4 | C． | 4$\sqrt{2}$ | D． | 8 |
5．已知命题P：?x∈R，x2+2x+2＜0，则￢P为（ ）
| A． | ?x∈R，x2+2x+2≥0，真命题 | B． | ?x∈R，x2+2x+2＜0，假命题 | ||
| C． | ?x∉R，x2+2x+2≥0，假命题 | D． | ?x∈R，x2+2x+2≥0，真命题 |
15．（重点中学做）已知x＞0，y＞0，2x+y+2xy=3，则2x+y的最小值是（ ）
| A． | 6 | B． | 3 | C． | 2 | D． | 1 |
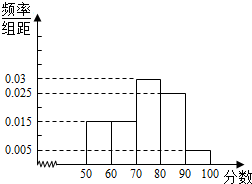为更好地迎接江苏省学业水平测试，某校针对本届高二文科学生，进行了物理学科模拟测试，从参加测试的学生中抽出60名学生，对他们的物理成绩进行统计（注：学生成绩均为整数且满分为100分），并把其中成绩不低于50分的分成五段：[50，60），[60，70）…[90，100]，画出如下部分频率分布直方图．请观察图形的相关信息，回答下列问题：