题目内容
18.求(x-3y+2z)100展开式的各项系数之和为( )| A. | 0 | B. | 1 | C. | -1 | D. | 9100 |
分析 令x=y=z=1,即可得出.
解答 解:令x=y=z=1,则(1-3+2)100=0,
∴(x-3y+2z)100展开式的各项系数之和为0.
故选:A.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
8.下列函数中,在区间(0,+∞)上为增函数的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-x2 | C. | y=($\frac{1}{2}$)x | D. | y=log2x |
7.在半径为5cm的圆中,圆心角为圆周角的$\frac{2}{3}$的角所对的圆弧长为( )
| A. | $\frac{4π}{3}$cm | B. | $\frac{20π}{3}$cm | C. | $\frac{10π}{3}$cm | D. | $\frac{50π}{3}$cm |
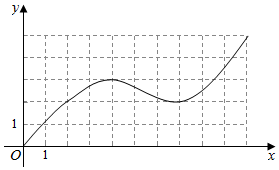 已知函数y=f(x)的图形如图所示,给出y=f(x)与x=10和x轴所围成图形的面积估计值;要想得到误差不超过1的面积估计值,可以怎么做?
已知函数y=f(x)的图形如图所示,给出y=f(x)与x=10和x轴所围成图形的面积估计值;要想得到误差不超过1的面积估计值,可以怎么做?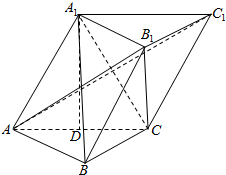 如图,三棱柱中ABC-A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1.
如图,三棱柱中ABC-A1B1C1中,点A1在平面ABC内的射影D为棱AC的中点,侧面A1ACC1为边长为2的菱形,AC⊥CB,BC=1.