题目内容
9.已知长为l(l≥1)的线段AB的两个端点在抛物线y=x2上滑动,则线段AB的中点M到x轴的距离的最小值是$\frac{1}{4}$.分析 设抛物线焦点为F,则AF+BF≥AB≥1,利用抛物线的性质将AF,BF转化为A,B到准线的距离来表示,得出A,B两点纵坐标的关系.
解答 解:抛物线y=x2的准线方程为y=-$\frac{1}{4}$,焦点坐标为F(0,$\frac{1}{4}$),
设A点纵坐标为y1,B点纵坐标为y2,则线段AB的中点M到x轴的距离为$\frac{{y}_{1}+{y}_{2}}{2}$.
∵A到准线的距离为y1+$\frac{1}{4}$=AF,B到准线的距离为y2+$\frac{1}{4}$=BF,
∵AF+BF≥AB≥1,∴y1+$\frac{1}{4}$+y2+$\frac{1}{4}$≥1,∴y1+y2≥$\frac{1}{2}$.∴$\frac{{y}_{1}+{y}_{2}}{2}$≥$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查了抛物线的性质,用A,B两点的纵坐标表示出到焦点的距离是解题关键,属于中档题.

练习册系列答案
相关题目
1.已知sinα=$\frac{\sqrt{3}}{2}$,cosβ=$-\frac{1}{3}$,且tanα•tanβ>0,则cos(α-β)的值是( )
| A. | -$\frac{1-2\sqrt{6}}{6}$ | B. | -$\frac{1+2\sqrt{6}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | ±$\frac{1+2\sqrt{6}}{6}$ |
18.求(x-3y+2z)100展开式的各项系数之和为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 9100 |
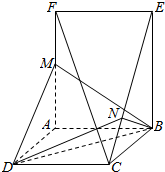 在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF上一点,N为CE上一点.
在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF上一点,N为CE上一点.