题目内容
13.已知cosθ=-$\frac{3}{5}$,θ∈($\frac{π}{2}$,π),求sin(θ+$\frac{π}{3}$)的值.分析 由同角三角函数基本关系可得sinθ,代入两角和的正弦公式计算可得.
解答 解:∵cosθ=-$\frac{3}{5}$,θ∈($\frac{π}{2}$,π),
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\frac{4}{5}$,
∴sin(θ+$\frac{π}{3}$)=sinθcos$\frac{π}{3}$+cosθsin$\frac{π}{3}$
=$\frac{4}{5}×\frac{1}{2}$+(-$\frac{3}{5}$)×$\frac{\sqrt{3}}{2}$=$\frac{4-3\sqrt{3}}{10}$
点评 本题考查两角和与差的正弦函数,涉及同角三角函数基本关系,属基础题.

练习册系列答案
相关题目
3.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2017年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{t}$.
1.已知sinα=$\frac{\sqrt{3}}{2}$,cosβ=$-\frac{1}{3}$,且tanα•tanβ>0,则cos(α-β)的值是( )
| A. | -$\frac{1-2\sqrt{6}}{6}$ | B. | -$\frac{1+2\sqrt{6}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | ±$\frac{1+2\sqrt{6}}{6}$ |
18.求(x-3y+2z)100展开式的各项系数之和为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 9100 |
5.已知直线y=x+b与两曲线C1:x2+y2-|x|-|y|=0和C2:x2+y2-|x|-|y|=$\frac{1}{2}$仅有两个交点,则实数b的取值范围是( )
| A. | (-2,2) | B. | (-1-$\sqrt{2}$,1+$\sqrt{2}$) | C. | (-1-$\sqrt{2}$,-$\sqrt{2}$)∪(-$\sqrt{2}$,1+$\sqrt{2}$) | D. | (-1-$\sqrt{2}$,-2)∪(2,1+$\sqrt{2}$) |
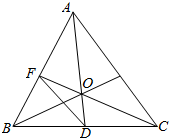 如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.
如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.