题目内容
3.已知a:b:c=2:$\sqrt{6}$:($\sqrt{3}$+1),求角A,B,C.分析 设a=2x,b=$\sqrt{6}$x,c=($\sqrt{3}+1$)x,由余弦定理可得cosA=$\frac{\sqrt{2}}{2}$,结合范围A∈(0,π),可得A,由余弦定理可得cosB=$\frac{1}{2}$,结合范围B∈(0,π),可得B,根据三角形内角和定理可求C的值.
解答 解:由题意,可设a=2x,b=$\sqrt{6}$x,c=($\sqrt{3}+1$)x,
由余弦定理可得:cosA=$\frac{6{x}^{2}+(4+2\sqrt{3}){x}^{2}-4{x}^{2}}{2×\sqrt{6}x×(\sqrt{3}+1)x}$=$\frac{\sqrt{2}}{2}$,由A∈(0,π),可得:A=$\frac{π}{4}$,
由余弦定理可得:cosB=$\frac{4{x}^{2}+(\sqrt{3}+1)^{2}{x}^{2}-6{x}^{2}}{2×2x×(\sqrt{3}+1)x}$=$\frac{1}{2}$,由B∈(0,π),可得:B=$\frac{π}{3}$,
可得:C=π-A-B=$\frac{5π}{12}$.
点评 本题主要考查了余弦定理,三角形内角和定理在解三角形中的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.求(x-3y+2z)100展开式的各项系数之和为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 9100 |
20.某几何体的三视图如图所示,在该几何体的各个面中,面积最小的面与底面的面积之比为( )
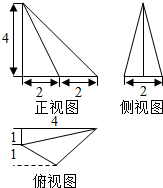

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |