题目内容
10.已知:$\overrightarrow{a}$=(2cosx,sinx),$\overrightarrow{b}$=($\sqrt{3}$cosx,2cosx),设函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$-$\sqrt{3}$(x∈R)求:(1)f(x)的最小正周期及最值;
(2)f(x)的对称轴及单调递增区间.
分析 (1)使用向量的数量积公式得出f(x)并化简,利用正弦函数的性质得出f(x)的周期和最值;
(2)令2x+$\frac{π}{3}$=$\frac{π}{2}+kπ$解出f(x)的对称轴,令-$\frac{π}{2}+2kπ$≤2x+$\frac{π}{3}$≤$\frac{π}{2}+2kπ$解出f(x)的增区间.
解答 解:(1)f(x)=2$\sqrt{3}$cos2x+2sinxcosx-$\sqrt{3}$=$\sqrt{3}$+$\sqrt{3}$cos2x+sin2x-$\sqrt{3}$=2sin(2x+$\frac{π}{3}$).
∴f(x)的最小正周期T=$\frac{2π}{2}$=π,f(x)的最大值为2,f(x)的最小值为-2.
(2)令2x+$\frac{π}{3}$=$\frac{π}{2}+kπ$得x=$\frac{π}{12}$+$\frac{kπ}{2}$,∴f(x)的对称轴为x=$\frac{π}{12}$+$\frac{kπ}{2}$.
令-$\frac{π}{2}+2kπ$≤2x+$\frac{π}{3}$≤$\frac{π}{2}+2kπ$,解得-$\frac{5π}{12}$+kπ≤x≤$\frac{π}{12}$+kπ,∴f(x)的单调增区间是[-$\frac{5π}{12}$+kπ,$\frac{π}{12}$+kπ],k∈Z.
点评 本题考查了三角函数的恒等变换和正弦函数的性质,属于中档题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
1.已知sinα=$\frac{\sqrt{3}}{2}$,cosβ=$-\frac{1}{3}$,且tanα•tanβ>0,则cos(α-β)的值是( )
| A. | -$\frac{1-2\sqrt{6}}{6}$ | B. | -$\frac{1+2\sqrt{6}}{6}$ | C. | $\frac{1+2\sqrt{6}}{6}$ | D. | ±$\frac{1+2\sqrt{6}}{6}$ |
18.求(x-3y+2z)100展开式的各项系数之和为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 9100 |
5.已知直线y=x+b与两曲线C1:x2+y2-|x|-|y|=0和C2:x2+y2-|x|-|y|=$\frac{1}{2}$仅有两个交点,则实数b的取值范围是( )
| A. | (-2,2) | B. | (-1-$\sqrt{2}$,1+$\sqrt{2}$) | C. | (-1-$\sqrt{2}$,-$\sqrt{2}$)∪(-$\sqrt{2}$,1+$\sqrt{2}$) | D. | (-1-$\sqrt{2}$,-2)∪(2,1+$\sqrt{2}$) |
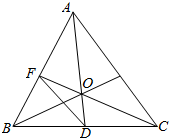 如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.
如图所示,已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{OD}$=$\overrightarrow{d}$,$\overrightarrow{OF}$=$\overrightarrow{f}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,$\overrightarrow{f}$表示下列向量.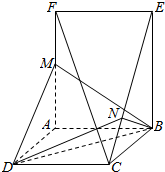 在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF上一点,N为CE上一点.
在如图所示的几何体中,正方形ABCD和矩形ABEF所在的平面互相垂直,M为AF上一点,N为CE上一点.