题目内容
14.已知集合A={x|-1≤x≤2},B={x|x2-4x≤0},则A∪B={x|-1≤x≤4},A∩(∁RB)={x|-1≤x<0}.分析 先求出集合A,B,再求出∁RB,由此能求出A∪B和 A∩(∁RB).
解答 解:∵集合A={x|-1≤x≤2},B={x|x2-4x≤0}={x|0≤x≤4},
∴∁RB={x|x<0或x>4},
∴A∪B={x|-1≤x≤4},A∩(∁RB)={x|-1≤x<0}.
故答案为:{x|-1≤x≤4},{x|-1≤x<0}.
点评 本题考查并集、补集、交集的求法,是基础题,解题时要认真审题,注意并集、补集、交集的定义的合理运用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.设Sn为等差数列{an}的前n项和,若$\frac{{S}_{1}}{{S}_{4}}$=$\frac{1}{10}$,则$\frac{{S}_{3}}{{S}_{5}}$=( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
6.函数f(x)=3sin(2x-$\frac{π}{3}$)的图象可以由y=3sin2x的图象( )
| A. | 向右平移$\frac{π}{3}$个单位长度得到 | B. | 向左平移$\frac{π}{3}$个单位长度得到 | ||
| C. | 向右平移$\frac{π}{6}$个单位长度得到 | D. | 向左平移$\frac{π}{6}$个单位长度得到 |
3.下面四个命题中的真命题是( )
| A. | 命题“?x≥2,均有x2-3x+2≥0”的否定是:“?x<2,使得x2-3x+2<0” | |
| B. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5、16、27、38、49的同学均被选出,则该班人数可能为60 | |
| D. | 在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.3,则X在(0,2)内取值的概率为0.6 |
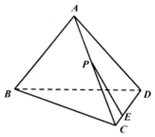 如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.
如图,已知三棱锥A-BCD的所有棱长均相等,点E满足$\overrightarrow{DE}$=3$\overrightarrow{EC}$,点P在棱AC上运动,设EP与平面BCD所成角为θ,则sinθ的最大值为$\frac{2\sqrt{2}}{3}$.