题目内容
7.已知两曲线f(x)=2sinx,g(x)=acosx,$x∈(0\;,\;\;\frac{π}{2})$相交于点P.若两曲线在点P处的切线互相垂直,则实数a的值为$\frac{{2\sqrt{3}}}{3}$.分析 联立两曲线方程,可得tanx=$\frac{sinx}{cosx}$=$\frac{a}{2}$,a>0,设交点P(m,n),分别求出f(x),g(x)的导数,可得切线的斜率,由两直线垂直的条件:斜率之积为-1,再由同角基本关系式,化弦为切,解方程即可得到a的值.
解答 解:由f(x)=g(x),即2sinx=acosx,
即有tanx=$\frac{sinx}{cosx}$=$\frac{a}{2}$,a>0,
设交点P(m,n),
f(x)=2sinx的导数为f′(x)=2cosx,
g(x)=acosx的导数为g′(x)=-asinx,
由两曲线在点P处的切线互相垂直,
可得2cosm•(-asinm)=-1,
且tanm=$\frac{a}{2}$,
则$\frac{2asinmcosm}{si{n}^{2}m+co{s}^{2}m}$=1,
分子分母同除以cos2m,
即有$\frac{2atanm}{1+ta{n}^{2}m}$=1,
即为a2=1+$\frac{{a}^{2}}{4}$,
解得a=$\frac{{2\sqrt{3}}}{3}$.
故答案为:$\frac{{2\sqrt{3}}}{3}$.
点评 本题考查导数的运用:求切线的斜率,两直线垂直的条件:斜率之积为-1,同时考查同角三角函数的基本关系式,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
18.已知x,y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ 5x-3y-12≥0\\ y≤3\end{array}\right.$当目标函数z=ax+by(a>0,b>0)在该约束条件下取得最小值1时,则$\frac{1}{3a}+\frac{2}{b}$的最小值为( )
| A. | $4+2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $3+2\sqrt{2}$ | D. | $3+\sqrt{2}$ |
19.已知复数z满足z(1+i)=1-i,则|z|=( )
| A. | i | B. | 1 | C. | -i | D. | -1 |
17.设集合A={-1,0,1,2},B={x|x-1<0},则A∩B=( )
| A. | (-1,1) | B. | (-1,0) | C. | {-1,0,1} | D. | {-1,0} |

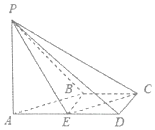 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.