题目内容
9．若关于x的方程4sin2x-msinx+1=0在（0，π）内有两个不同的实数解，则实数m的取值范围为（ ）| A． | m＞4或m＜-4 | B． | 4＜m＜5 | C． | 4＜m＜8 | D． | m＞5或m=4 |
分析 利用换元法，结合三角函数的性质以及一元二次方程与一元二次函数之间的关系进行求解即可．
解答 解：设t=sinx，则0＜t≤1，
则方程等价为f（t）=4t2-mt+1=0在（0，1]内有唯一解，
即$\left\{\begin{array}{l}{△={m}^{2}-16=0}\\{\frac{m}{8}＞0}\end{array}\right.$或f（1）=5-m＜0，
得m=4或m＞5．
故选：D．
点评 本题主要考查函数与方程的应用，利用换元法转化为一元二次函数和一元二次方程是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．m，n，l为不重合的直线，α，β，γ为不重合的平面，则下列说法正确的是（ ）
| A． | α∥γ，β∥γ，则α∥β | B． | α⊥γ，β⊥γ，则α⊥β | C． | m∥α，n∥α，则m∥n | D． | m⊥l，n⊥l，则m∥n |
4．
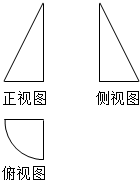一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为2的直角三角形，俯视图是半径为1的$\frac{1}{4}$圆周和两条半径，则这个几何体的体积为（ ）
一个几何体的三视图如图所示，其中正视图与侧视图都是斜边长为2的直角三角形，俯视图是半径为1的$\frac{1}{4}$圆周和两条半径，则这个几何体的体积为（ ）| A． | $\frac{\sqrt{3}}{12}$π | B． | $\frac{\sqrt{3}}{6}$π | C． | $\frac{\sqrt{3}}{4}$π | D． | $\frac{\sqrt{3}}{3}$π |
14．已知复数z满足z（1-$\sqrt{3}$i）=4（i为虚数单位），则z=（ ）
| A． | -2-2$\sqrt{3}$i | B． | 1+$\sqrt{3}$i | C． | -1-$\sqrt{3}$i | D． | 1-$\sqrt{3}$i |
18．若$\left\{\begin{array}{l}{x-y≤0}\\{x+y≤1}\\{x≥0}\end{array}\right.$，则z=x+2y的最小值为（ ）
| A． | -1 | B． | 0 | C． | $\frac{3}{2}$ | D． | 2 |