题目内容
14．已知复数z满足z（1-$\sqrt{3}$i）=4（i为虚数单位），则z=（ ）| A． | -2-2$\sqrt{3}$i | B． | 1+$\sqrt{3}$i | C． | -1-$\sqrt{3}$i | D． | 1-$\sqrt{3}$i |
分析 直接由复数代数形式的乘除运算化简复数z，则答案可求．
解答 解：由z（1-$\sqrt{3}$i）=4，
得$z=\frac{4}{1-\sqrt{3}i}=\frac{4（1+\sqrt{3}i）}{（1-\sqrt{3}i）（1+\sqrt{3}i）}=1+\sqrt{3}i$．
故选：B．
点评 本题考查了复数代数形式的乘除运算，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．设x∈R，则“-1＜x＜6”是“2x2-5x-3＜0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
9．若关于x的方程4sin2x-msinx+1=0在（0，π）内有两个不同的实数解，则实数m的取值范围为（ ）
| A． | m＞4或m＜-4 | B． | 4＜m＜5 | C． | 4＜m＜8 | D． | m＞5或m=4 |
19．在5张电话卡中，有3张移动卡和2张联通卡，从中任取2张，若事件“2张全是移动卡”的概率是$\frac{3}{10}$，那么概率是$\frac{7}{10}$的事件是（ ）
| A． | 至多有一张移动卡 | B． | 恰有一张移动卡 | ||
| C． | 都不是移动卡 | D． | 至少有一张移动卡 |
6．已知集合M={1，2，3，4}，N={（a，b）|a∈M，b∈M}，A是集合N中任意一点，O为坐标原点，则直线OA与y=x2+1有交点的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{8}$ |
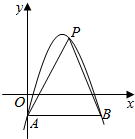姐图，在平面直角坐标系中，抛物线y=-（x-2）2+3与y轴交于点A，过点A与x轴平行的直线交抛物线于另一点B，点P是直线AB上方的抛物线上一点，设点P的横坐标为m，则△PAB的面积S的取值范围为0＜S≤8．