题目内容
在数列{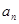 }中,
}中,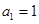 ,
,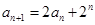 ,设
,设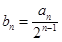 ,
,
(1)证明:数列{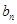 }是等差数列;
}是等差数列;
(2)求数列{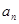 }的前n项和
}的前n项和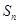 ;
;
(3)设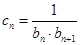 ,证明:
,证明: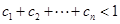
(1)证明如下(2)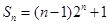
(3)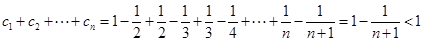
解析试题分析:(1)证明:由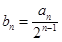 得:
得: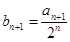
又因为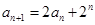 ,所以
,所以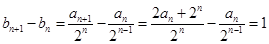
所以数列{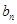 }是等差数列
}是等差数列
(2)数列{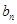 }的首项是:
}的首项是: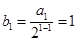 ,
,
又因为公差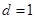 ,所以
,所以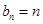
由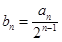 得:
得: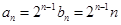
所以数列{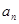 }的前n项和
}的前n项和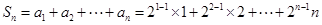
所以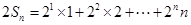
两式相减得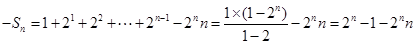
所以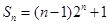
(3)因为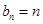 ,所以
,所以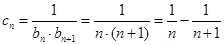
所以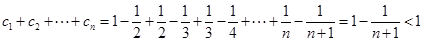
考点:等差数列的定义;数列的前n项和
点评:对于求一般数列的通项公式或前n项和时,常用方法有:错位相减法、裂变法等,目的是消去中间部分,本题在求前n项和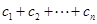 时就用到裂变法。
时就用到裂变法。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,将函数
,将函数 在区间
在区间 内的全部极值点按从小到大的顺序排成数列
内的全部极值点按从小到大的顺序排成数列
 .
. ,数列
,数列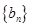 的前
的前 项和为
项和为 ,求
,求 是等差数列,且
是等差数列,且 ,
, .
.
 ,求数列
,求数列 的前
的前 项和.
项和.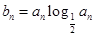 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.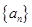 的前
的前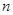 项和为
项和为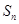 ,若
,若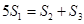 ,且
,且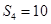 求数列
求数列 中,
中, ,公比
,公比 .
. 为
为
 ,求数列
,求数列 的通项公式.
的通项公式.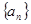 的首项为
的首项为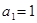 ,其前
,其前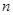 项和为
项和为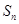 ,且对任意正整数
,且对任意正整数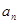 、
、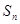 成等差数列.
成等差数列.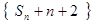 成等比数列;
成等比数列; 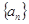 中,已知
中,已知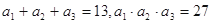 ,且公比为正整数.
,且公比为正整数. 的通项公式;(5分)
的通项公式;(5分) 项和.(5分)
项和.(5分)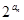 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn.