题目内容
10.设直线l 的倾斜角α满足α∈($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$),则直线l 的斜率k 的取值范围为(-∞,-1)∪(1,+∞).分析 由已知利用正切函数的性质,得到直线l的斜率k的取值范围.
解答 解:∵直线l的倾斜角为α,且α∈($\frac{π}{4}$,$\frac{π}{2}$)∪($\frac{π}{2}$,$\frac{3π}{4}$),
∴直线l的斜率k的取值范围是:k<-1或k>1,
即直线l的斜率k的取值范围是(-∞,-1)∪(1,+∞).
故答案为(-∞,-1)∪(1,+∞).
点评 本题考查直线的斜率的取值范围的求法,是基础题,解题时要注意正切函数的性质的合理运用.

练习册系列答案
相关题目
20.已知函数f(x)=$\frac{2x}{{{x^2}+1}}$,则下列说法正确的是( )
| A. | 函数f(x)在(0,+∞)上有最小值 | B. | 函数f(x)在(0,+∞)上没有最大值 | ||
| C. | 函数f(x)在R上没有极小值 | D. | 函数f(x)在R上有极大值 |
7.命题:“?x∈R,x2+mx+2≤0”为假命题,是命题|m-1|<2的( )
| A. | 充分不必要条件 | B. | 必要非充分条件 | C. | 充要条件 | D. | 都不是 |
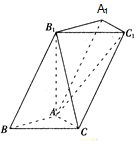 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°. 如图,在平面直角坐标系xOy中,点A,B,C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.
如图,在平面直角坐标系xOy中,点A,B,C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.