题目内容
13.已知点(x,y)满足$\left\{\begin{array}{l}x+2y-8≥0\\ 2x-y-6≤0\\ x-3y+7≥0\end{array}\right.$,则$z=\frac{x+1}{y-1}$的取值范围为( )| A. | $[{\frac{3}{2},5}]$ | B. | $[{\frac{2}{3},5}]$ | C. | $[{\frac{3}{2},7}]$ | D. | $[{\frac{2}{3},7}]$ |
分析 首先画出可行域,利用z的几何意义:区域内的点与(-1,1)连接直线的斜率的倒数,因此求最值即可.
解答 解:由已知得到平面区域如图: $z=\frac{x+1}{y-1}$表示区域内的点与(-1,1)连接的直线斜率的倒数,当与A(2,3)连接时直线斜率最大为$\frac{3-1}{2+1}=\frac{2}{3}$,与B(4,2)连接时直线斜率最小为$\frac{2-1}{4+1}=\frac{1}{5}$,
$z=\frac{x+1}{y-1}$表示区域内的点与(-1,1)连接的直线斜率的倒数,当与A(2,3)连接时直线斜率最大为$\frac{3-1}{2+1}=\frac{2}{3}$,与B(4,2)连接时直线斜率最小为$\frac{2-1}{4+1}=\frac{1}{5}$,
所以$z=\frac{x+1}{y-1}$的最大值为5,最小值为$\frac{3}{2}$,所以$z=\frac{x+1}{y-1}$的取值范围为[$\frac{3}{2}$,5];
故选:A.
点评 本题考查了简单线性规划问题;一般的,首先正确画出可行域,然后根据目标函数的几何意义求最值;体现了数形结合的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
8.已知命题p:?x0<0,sinx0>0且tanx0>0,则命题p的否定为( )
| A. | ?x<0,sinx≤0或tanx≤0 | B. | ?x<0,sinx≤0且tanx≤0 | ||
| C. | ?x≥0,sinx≤0或tanx≤0 | D. | ?x≥0,sinx≤0且tanx≤0 |
7.命题:“?x∈R,x2+mx+2≤0”为假命题,是命题|m-1|<2的( )
| A. | 充分不必要条件 | B. | 必要非充分条件 | C. | 充要条件 | D. | 都不是 |
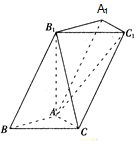 已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.
已知三棱柱ABC-A1B1C1中,AA1=B1C=2AB=2AC=2,∠BAC=90°,∠BAA1=120°.