题目内容
设函数f(x)=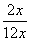 -
-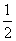 ,[x]表示不超过x的最大整数,则函数y=[f(x)]的值域是( ).
,[x]表示不超过x的最大整数,则函数y=[f(x)]的值域是( ).
A.{0,1} B.{0,-1} C.{-1,1} D.{1,1}
B
解析 由f(x)=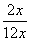 -
-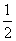 =1-
=1- -
-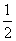 =
=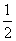 -
- ,
,
由于(2x+1)在R上单调递增,所以- 在R上单调递增,所以f(x)为增函数,由于2x>0,当x→-∞,2x→0,
在R上单调递增,所以f(x)为增函数,由于2x>0,当x→-∞,2x→0,
∴f(x)>-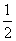 ,当x→+∞,
,当x→+∞, →0,
→0,
∴f(x)<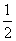 ,∴-
,∴-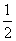 <f(x)<
<f(x)<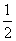 ,
,
∴y=[f(x)]={0,-1}.

练习册系列答案
相关题目
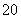 +2ax0+2a≤0,若命题“p∨q”是假命题,求a的取值范围.
+2ax0+2a≤0,若命题“p∨q”是假命题,求a的取值范围. ,2)在幂函数y=f(x)的图象上,点
,2)在幂函数y=f(x)的图象上,点 在幂函数y=g(x)的图象上,若f(x)=g(x),则x=________.
在幂函数y=g(x)的图象上,若f(x)=g(x),则x=________.
 ,b=log
,b=log ,c=log3
,c=log3 ,则a、b、c的大小关系是( )
,则a、b、c的大小关系是( ) 的图象大致为( )
的图象大致为( )