题目内容
在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，PA=AC=BC，则PC与AB成角的大小是（ ）
| A、30° | B、60° |
| C、120° | D、90° |
考点：异面直线及其所成的角
专题：空间角
分析：以C为原点，CB为x轴，CA为y轴，建立空间直角坐标系，设PC与AB成角的大小为θ，由cosθ=|cos＜
，
＞|=
能求出PC与AB成角的大小．
| PC |
| AB |
|
| ||||
|
|
解答：
解：以C为原点，CB为x轴，CA为y轴，建立空间直角坐标系，
设PA=AC=BC，
则P（0，1，1），C（0，0，0），
A（0，1，0），B（1，0，0），
=（0，-1，-1），
=（1，-1，0），
设PC与AB成角的大小为θ，
cosθ=|cos＜
，
＞|=
=
=
，
∴θ=60°．
∴PC与AB成角的大小为60°．
故选：B．
解：以C为原点，CB为x轴，CA为y轴，建立空间直角坐标系，设PA=AC=BC，
则P（0，1，1），C（0，0，0），
A（0，1，0），B（1，0，0），
| PC |
| AB |
设PC与AB成角的大小为θ，
cosθ=|cos＜
| PC |
| AB |
|
| ||||
|
|
=
| 1 | ||||
|
| 1 |
| 2 |
∴θ=60°．
∴PC与AB成角的大小为60°．
故选：B．
点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意向量法的合理运用．
练习册系列答案
相关题目
曲线f（x）=ex+x2+x+1上的点到直线2x-y=3的距离的最小值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
设R表示实数集，A=[-1，2]，B=（0，+∞），则A∩∁RB等于（ ）
| A、（0，2] |
| B、（-∞，2] |
| C、（-1，+∞） |
| D、[-1，0] |
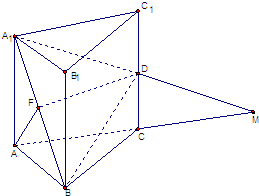已知：正三棱柱A1B1C1-ABC中，AA1=AB=a，D为CC1的中点，F是A1B的中点，A1D与AC的延长线交于点M．
如图所示的几何体中，四边形ABCD与BDEF是边长均为a的菱形，FA=FC