题目内容
19.空间四边形ABCD中,对角线AC与BD互相垂直,那么顺次联结四边形各边中点所得的四边形是矩形.分析 根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.
解答 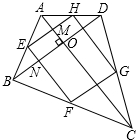 已知:AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
已知:AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
求证:四边形EFGH是矩形
证明:∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,(三角形的中位线平行于第三边)
∴四边形EFGH是平行四边形,(两组对边分别平行的四边形是平行四边形)
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故答案为:矩形.
点评 本题考查的是矩形的判定方法,常用的方法有三种:
①一个角是直角的平行四边形是矩形.
②三个角是直角的四边形是矩形.
③对角线相等的平行四边形是矩形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若a,b,p(a≠0,b≠0,p>0)分别表示同一直线的横截距、纵截距及原点到直线的距离,则下列关系式成立的是( )
| A. | $\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{p}^{2}}$ | B. | $\frac{1}{{a}^{2}}$-$\frac{1}{{b}^{2}}$=$\frac{1}{{p}^{2}}$ | C. | $\frac{1}{{a}^{2}}$+$\frac{1}{{p}^{2}}$=$\frac{1}{{b}^{2}}$ | D. | $\frac{1}{{a}^{2}{p}^{2}}$=$\frac{1}{{b}^{2}}$ |