题目内容
7.袋子里装有编号分别为“1、2、2、3、4、5”的6个大小、质量相同的小球,某人从袋子中一次任取3个球,若每个球被取到的机会均等,则取出的3个球编号之和大于7的概率为( )| A. | $\frac{17}{20}$ | B. | $\frac{7}{10}$ | C. | $\frac{5}{8}$ | D. | $\frac{4}{5}$ |
分析 基本事件总数n=${C}_{6}^{3}$=20,利用列举法求出取出的3个球编号之和不大于7的基本事件个数,由此能求出取出的3个球编号之和大于7的概率.
解答 解:袋子里装有编号分别为“1、2、3、4、5”的6个大小、质量相同的小球,
某人从袋子中一次任取3个球,每个球被取到的机会均等,
基本事件总数n=${C}_{6}^{3}$=20,
取出的3个球编号之和不大于7的基本事件有:
122,123,123,124,124,223,共有6个,
∴取出的3个球编号之和大于7的概率为:
p=1-$\frac{6}{20}$=$\frac{7}{10}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法、对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
12.下列函数中为偶函数的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=x3 | C. | y=$\sqrt{x}$ | D. | y=ex+e-x |
17.函数f(x)=ax2+2(a-3)x+1在区间[-2,+∞)上递减,则实数a的取值范围是( )
| A. | (-∞,0) | B. | [-3,+∞) | C. | [-3,0] | D. | (0,+∞) |
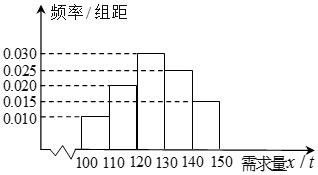 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.