题目内容

在△ABC中，cosA=
7
25
，A=2B，∠A的平分线AD的长为10．
（1）求B的余弦值；
（2）求AC的边长．
考点：余弦定理
专题：解三角形
分析：（1）由cosA=
7
25
，A=2B，可得cos2B=
7
25
=2cos2B-1，解出即可．
（2）过点D作DE⊥AB，垂足为E，则点E为AB的中点．可得BD=AD=10，cosB=
4
5
，BE=BDcosB=8=AE．可得DE=6．利用角平分线的性质可得
AB
AC
=
BD
DC
，因此
AB
AB+AC
=
BD
BC
=
BE
AB
=
1
2
，即可得出．
解答： 解：（1）∵cosA=
7
25
，A=2B，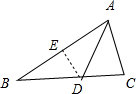
∴cos2B=
7
25
=2cos2B-1，cosB＞0，cosB=
4
5
．
（2）过点D作DE⊥AB，垂足为E，则点E为AB的中点．
∵BD=AD=10，cosB=
4
5
，
∴BE=BDcosB=8=AE．
∴DE=
BD2-AE2
=6．
∵
AB
AC
=
BD
DC
，
∴
AB
AB+AC
=
BD
BC
=
BE
AB
=
1
2
，
解得AB=AC=16．
点评：本题考查了倍角公式、直角三角形的边角关系、勾股定理、角平分线的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
在数列{an}中，已知（n2+n）an+1=（n2+2n+1）an，n∈N+，且a1=1，求an的表达式．
下列结论中正确的是（　　）
①命题：?x∈（0，2），3x＞x3的否定是?x∈（0，2），3x≤x3；
②若直线l上有无数个点不在平面α内，则l∥α；
③若随机变量ξ服从正态分布N（1，σ2），且P（ξ＜2）=0.8，则P（0＜ξ＜1）=0.2；
④等差数列{an}的前n项和为Sn，若a4=3，则S7=21．
A、①②B、②③C、③④D、①④
焦点在x轴上的双曲线C的左焦点为F，右顶点为 A，若线段F A的中垂线与双曲线C相切，则双曲线C的离心率是（　　）
A、2
B、
2
C、3
D、
3
已知函数f（x）=xcos
πx
λ
，存在f（x）的零点x0，（x0≠0），满足[f′（x0）]2＜π2（λ2-x02），则λ的取值范围是（　　）
A、（-
3
，0）∪（0，
3
，）
B、（-
3
3
，0）∪（0，
3
3
）
C、（-∞，-
3
）∪（
3
，+∞）
D、（-∞，-
3
3
）∪（
3
3
，+∞）
某程序框图如图所示，则输出的S等于（　　）
A、6B、14C、30D、32
在平面直角坐标系中，△ABC的两个顶点A，B的坐标分别是（-
2
，0），（
2
，0），点G是△ABC的重心，y轴上一点M满足GM∥AB，且|MC|=|MB|．
（Ⅰ）求△ABC的顶点C的轨迹E的方程；
（Ⅱ）不过点A的直线l与轨迹E交于不同的两点P，Q．若以PQ为直径的圆过点A时，试判断直线l是否过定点？若过，请求出定点坐标，不过，说明理由．
已知函数f（x）=2sin（ωx-
π
3
）cosωx+
3
2
（ω＞0）的最小正周期为π．
（1）求f（x）的值域；
（2）已知在△ABC中，角A，B，C的对边分别为a，b，c，若f（
A
2
）=
3
2
，b+c=2，求a的最小值．
“任何三角形的外角都至少有两个钝角”的否定应是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网