题目内容
定义函数f(x)=
,则函数g(x)=xf(x)-6在区间[1,2n](n∈N*)内的所有零点的和为( )
|
| A、n | ||
| B、2n | ||
C、
| ||
D、
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:函数f(x)是分段函数,要分区间进行讨论,当1≤x≤2,f(x)是二次函数,当x>2时,对应的函数很复杂,找出其中的规律,最后作和求出.
解答:
解:当1≤x≤
时,f(x)=8x-8,
所以g(x)=8(x-
)2-8,此时当x=
时,g(x)max=0;
当
<x≤2时,f(x)=16-8x,所以g(x)=-8(x-1)2+2<0;
由此可得1≤x≤2时,g(x)max=0.
下面考虑2n-1≤x≤2n且n≥2时,g(x)的最大值的情况.
当2n-1≤x≤3•2n-2时,由函数f(x)的定义知f(x)=
f(
)=…=
f(
),
因为1≤
≤
,
所以g(x)=
(x-2n-2)2-8,
此时当x=3•2n-2时,g(x)max=0;
当3•2n-2≤x≤2n时,同理可知,g(x)=-
(x-2n-1)2+8<0.
由此可得2n-1≤x≤2n且n≥2时,g(x)max=0.
综上可得:对于一切的n∈N*,函数g(x)在区间[2n-1,2n]上有1个零点,
从而g(x)在区间[1,2n]上有n个零点,且这些零点为xn=3•2n-2,因此,所有这些零点的和为
(2n-1).
故选:D
| 3 |
| 2 |
所以g(x)=8(x-
| 1 |
| 2 |
| 3 |
| 2 |
当
| 3 |
| 2 |
由此可得1≤x≤2时,g(x)max=0.
下面考虑2n-1≤x≤2n且n≥2时,g(x)的最大值的情况.
当2n-1≤x≤3•2n-2时,由函数f(x)的定义知f(x)=
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 2n-1 |
| x |
| 2n-1 |
因为1≤
| x |
| 2n-1 |
| 3 |
| 2 |
所以g(x)=
| 1 |
| 22n-5 |
此时当x=3•2n-2时,g(x)max=0;
当3•2n-2≤x≤2n时,同理可知,g(x)=-
| 1 |
| 22n-5 |
由此可得2n-1≤x≤2n且n≥2时,g(x)max=0.
综上可得:对于一切的n∈N*,函数g(x)在区间[2n-1,2n]上有1个零点,
从而g(x)在区间[1,2n]上有n个零点,且这些零点为xn=3•2n-2,因此,所有这些零点的和为
| 3 |
| 2 |
故选:D
点评:本题属于根的存在性及根的个数的判断的问题,是一道较复杂的问题,首先它是分段函数,各区间上的函数又很复杂,挑战人的思维和耐心.

练习册系列答案
相关题目
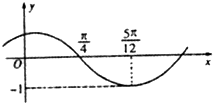 从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<
从函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|<| π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
点P(a,10)与圆(x-1)2+(y-1)2=2的位置关系是( )
| A、在圆外 | B、在圆内 |
| C、在圆上 | D、与a的值有关 |
要得到函数y=sin(2x+
)的图象,只要将函数y=cos2x的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
炼钢时钢水的含碳量与冶炼时间有( )
| A、确定性关系 | B、相关关系 |
| C、函数关系 | D、无任何关系 |
 在一次演讲比赛中,七位评委为某选手打出的分数的茎叶图(如图所示),去掉一个最高分一个最低分后,所剩数据的方差为
在一次演讲比赛中,七位评委为某选手打出的分数的茎叶图(如图所示),去掉一个最高分一个最低分后,所剩数据的方差为