题目内容
17．函数f（x）=$\frac{2}{x}$-log3x的零点所在的一个区间是（ ）| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
分析 确定函数的定义域为（0，+∞）与单调性，再利用零点存在定理，即可得到结论．
解答 解：函数的定义域为（0，+∞）
易知函数在（0，+∞）上单调递减，
∵f（2）=$\frac{2}{2}$-log32＞0，f（3）=$\frac{2}{3}$-log33＜0，
∴f（x）=$\frac{2}{x}$-log3x的零点所在的一个区间（2，3），
故选：C．
点评 本题考查函数的单调性，考查零点存在定理，属于基础题．
练习册系列答案
相关题目
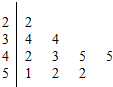近日有媒体在全国范围开展“2015年国人年度感受”的调查，在某城市广场有记者随机访问10个步行的路人，其年龄的茎叶图如下：
6．下列函数中，与函数y=2x表示同一函数的是（ ）
| A． | y=$\frac{2{x}^{2}}{x}$ | B． | y=$\sqrt{4{x}^{2}}$ | C． | y=（$\sqrt{2x}$）2 | D． | y=log24x |