题目内容
4.在平行四边形ABCD中,$\overrightarrow{AB}$•$\overrightarrow{BD}$=0,|$\overrightarrow{AB}$|=1,|$\overrightarrow{AD}$|=$\sqrt{3}$,若将其沿BD折成直二面角A-BD-C,则三棱锥A-BDC的外接球的表面积为( )| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
分析 折叠之后呢得出三棱锥A-BDC的外接球与长方体的外接球相同,利用对角线求解即可,再利用面积公式求解即可.
解答 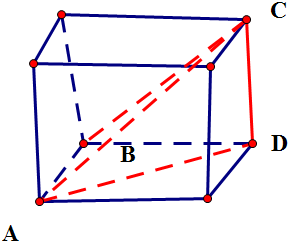 解:在平行四边形ABCD中,AB⊥BD,|$\overrightarrow{AB}$|=1,
解:在平行四边形ABCD中,AB⊥BD,|$\overrightarrow{AB}$|=1,
|$\overrightarrow{AD}$|=$\sqrt{3}$,若将其沿BD折成直二面角A-BD-C,
∴三棱锥A-BDC镶嵌在长方体中,
即得出:三棱锥A-BDC的外接球与长方体的外接球相同,
∴2R=$\sqrt{3+1}$=2,R=1,
∴外接球的表面积为4π×12=4π,
故选:C.
点评 本题考察了空间几何体的性质,空间思维能力的运用,镶嵌几何体的求解方法,转为常见的几何体求解,属于中档题.

练习册系列答案
相关题目
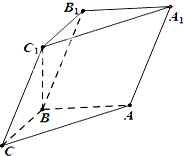 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=$\frac{π}{3}$.