题目内容
12.已知函数g(x)=$\frac{lnx}{x}$.(Ⅰ)求函数y=g(x)的图象在x=$\frac{1}{e}$处的切线方程;
(Ⅱ)令f(x)=ax2+bx-x•(g(x))(a,b∈R).
①若a≥0,求f(x)的单调区间;
②设a>0,且对任意x>0,f(x)≥f(1).试比较lna与-2b的大小.
分析 (Ⅰ)求出函数的导数,计算g′($\frac{1}{e}$)和g($\frac{1}{e}$)代入切线方程求出切线方程即可;
(Ⅱ)求出f(x)的导数,①通过讨论a的范围以及b的范围,求出函数的单调区间即可;②求出函数的极小值点,得到b=1-2a,通过讨论x的范围判断即可.
解答 解:(Ⅰ)$g'(x)=\frac{1-lnx}{x^2}$$g'(\frac{1}{e})=\frac{1+1}{{\frac{1}{e^2}}}=2{e^2}$,$g(\frac{1}{e})=-e$
所以切线方程为$y+e=2{e^2}(x-\frac{1}{e})$即2e2x-y-3e=0…(3分)
(Ⅱ)由f(x)=ax2+bx-lnx,x∈(0,+∞),得f'(x)=$\frac{{2a{x^2}+bx-1}}{x}$.
①(i)当a=0时,f'(x)=$\frac{bx-1}{x}$.
若b≤0,当x>0时,f'(x)<0恒成立,
所以函数f(x)的单调递减区间是(0,+∞).
若b>0,当0<x<$\frac{1}{b}$时,f'(x)<0,函数f(x)单调递减.
当x>$\frac{1}{b}$时,f'(x)>0,函数f(x)单调递增.
所以函数f(x)的单调递减区间是(0,$\frac{1}{b}$),单调递增区间是($\frac{1}{b}$,+∞)…(6分)
(ii)当a>0时,令f'(x)=0,得2ax2+bx-1=0.
由△=b2+8a>0得x1=$\frac{{-b-\sqrt{{b^2}+8a}}}{4a}$,x2=$\frac{{-b+\sqrt{{b^2}+8a}}}{4a}$.
显然,x1<0,x2>0.
当0<x<x2时,f'(x)<0,函数f(x)单调递减;
当x>x2时,f'(x)>0,函数f(x)单调递增.
所以函数f(x)的单调递减区间是(0,x2),单调递增区间是(x2,+∞).…(9分)
综上所述,
当a=0,b≤0时,函数f(x)的单调递减区间是(0,+∞);
当a=0,b>0时,函数f(x)的单调递减区间是(0,$\frac{1}{b}$),单调递增区间是($\frac{1}{b}$,+∞);
当a>0时,函数f(x)的单调递减区间是(0,x2),单调递增区间是(x2,+∞).…(10分)
②由题意,函数f(x)在x=1处取得最小值,
由(1)知$\frac{{-b+\sqrt{{b^2}+8a}}}{4a}$是f(x)的唯一极小值点,
故$\frac{{-b+\sqrt{{b^2}+8a}}}{4a}$=1,整理得2a+b=1,即b=1-2a.
令ϕ(x)=2-4x+lnx,则ϕ'(x)=$\frac{1-4x}{x}$,ϕ'(x)=0,得x=$\frac{1}{4}$.
当0<x<$\frac{1}{4}$时,ϕ'(x)>0,ϕ(x)单调递增;
当x>$\frac{1}{4}$时,ϕ'(x)<0,ϕ(x)单调递减.
因此ϕ(x)≤$ϕ(\frac{1}{4})$=1+$ln\frac{1}{4}$=1-ln4<0,
故ϕ(a)<0,即2-4a+lna=2b+lna<0,
即lna=-2b.…(14分)
点评 本题考查了函数的单调性、最值、极值问题,考查导数的应用以及分类讨论思想,是一道综合题.

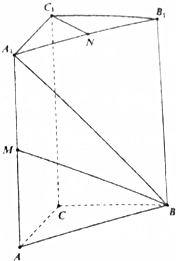 如图所示,在直三棱柱ABC-A1B1C1中,已知CA⊥CB,CA=CB=1,AA1=2,且棱AA1和A1B1的中点分别是M,N.
如图所示,在直三棱柱ABC-A1B1C1中,已知CA⊥CB,CA=CB=1,AA1=2,且棱AA1和A1B1的中点分别是M,N.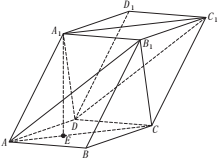 如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.
如图,棱柱ABCD-A1B1C1D1的底面是菱形.侧棱长为5,平面ABCD⊥平面A1ACC1,AB=3$\sqrt{3}$,∠BAD=60°,点E是△ABD的重心,且A1E=4.