题目内容
15.已知函数f(x)=$\frac{{m{x^2}+ax}}{{1+{x^2}}}$是奇函数.(1)求m的值;
(2)若f(x)=$\frac{{m{x^2}+ax}}{{1+{x^2}}}$在(1,+∞)上递减,根据单调性的定义求实数a的取值范围.
分析 (1)根据函数奇偶性的定义求出m的值即可;(2)根据函数单调性的定义求出a的范围即可.
解答 解:(1)∵函数$f(x)=\frac{{m{x^2}+ax}}{{{x^2}+1}}$是奇函数
∴f(-x)=-f(x).-------------------------------(2分)
∴$\frac{{m{x^2}-ax}}{{{x^2}+1}}=-\frac{{m{x^2}+ax}}{{{x^2}+1}}$,得m=0.-----------------(6分)
(2)∵$f(x)=\frac{ax}{{1+{x^2}}}$在(1,+∞)上递减
∴任给实数x1,x2,当1<x1<x2时f(x1)>f(x2)---------(7分)
∴$f({x_1})-f({x_2})=\frac{{a{x_1}}}{{1+{x_1}^2}}-\frac{{a{x_2}}}{{1+{x_2}^2}}=\frac{{a({x_1}-{x_2})(1-{x_1}{x_2})}}{{(1+{x_1}^2)(1+{x_2}^2)}}>0-----(10分)$
∴a<0------------------------------------------------------(12分)
点评 本题考查了函数的单调性、奇偶性问题,是一道中档题.

练习册系列答案
相关题目
20.在平行四边形ABCD中,$\overrightarrow{AB}+\overrightarrow{AD}$=( )
| A. | $\overrightarrow{AC}$ | B. | $\overrightarrow{BD}$ | C. | $\overrightarrow{CA}$ | D. | $\overrightarrow{DB}$ |
5.若集合M={x|log2x<1},集合N={x|x2-1≤0},则M∩N=( )
| A. | {x|1≤x<2} | B. | {x|-1≤x<2} | C. | {x|-1<x≤1} | D. | {x|0<x≤1} |
 已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$.
已知P(0,-1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足$\overrightarrow{PF}$=7$\overrightarrow{FQ}$.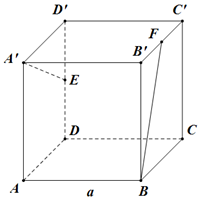 如图正方体ABCD-A′B′C′D′中,E、F为中点,
如图正方体ABCD-A′B′C′D′中,E、F为中点,