题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,判断
,判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(3)若![]() ,
,![]() ,
,![]() 有三个不同实根,求
有三个不同实根,求![]() 的取值范围.
的取值范围.
【答案】(1)奇函数;(2)0;(3)![]() .
.
【解析】
(1)由![]() 判断即可得解;
判断即可得解;
(2)由分段函数求值域问题分![]() ,
,![]() ,
,![]() ,
,![]() ,讨论即可;
,讨论即可;
(3)由方程与函数的关系可得![]() 有三个不同实根,等价于函数
有三个不同实根,等价于函数![]() 与直线
与直线![]() 有三个交点,通过求函数
有三个交点,通过求函数![]() 的单调性及值域即可得解.
的单调性及值域即可得解.
解:(1)当![]() 时,
时,![]() ,
,
则![]() ,
,
故![]() 为奇函数;
为奇函数;
(2)当![]() 时,
时,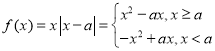 ,
,
又![]() ,
,
①当![]() 时,可得函数
时,可得函数![]() 在
在![]() 为增函数,可得
为增函数,可得![]() ;
;
②当![]() 时,可得函数
时,可得函数![]() 在
在![]() 为增函数,在
为增函数,在![]() 为减函数,
为减函数,
由![]() ,
,
可得当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ;
;
③当![]() 时,由
时,由![]() ,可得
,可得![]() ;
;
综上可得:当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上的最小值为即
上的最小值为即![]() ;
;
(3)因为![]() ,且
,且![]() 有三个不同实根,
有三个不同实根,
则函数![]() 不单调,且
不单调,且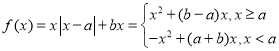 ,
,
因为![]() ,又
,又![]() ,
,![]() ,
,
所以当![]() 时,函数为增函数,则
时,函数为增函数,则![]() 时,函数不单调,要使函数
时,函数不单调,要使函数![]() 有三个不同实根,则
有三个不同实根,则![]() ,即
,即![]() ,即
,即![]() ,
,
故![]() ,
,
故![]() 的取值范围为:
的取值范围为:![]() .
.

练习册系列答案
相关题目
【题目】作为交通重要参与者的行人,闯红灯通行频有发生,带来了较大的交通安全隐患.在某十字路口,交警部门从穿越该路口的行人中随机抽取了200人进行调查,得到不完整的![]() 列联表如图所示:
列联表如图所示:
年龄低于30岁 | 年龄不低于30岁 | 合计 | |
闯红灯 | 60 | 80 | |
未闯红灯 | 80 | ||
合计 | 200 |
(1)将![]() 列联表补充完整;
列联表补充完整;
(2)是否有99.9%的把握认为行人是否闯红灯与年龄有关.
参考公式及数据: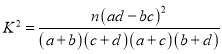 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |