题目内容
【题目】函数
是定义在
上的奇函数，且
为偶函数，当
时，
，若
有三个零点，则实数
的取值集合是________.
【答案】
【解析】
先根据条件判断函数
的对称性和周期性，再求出函数在一个周期内的解析式；要求
的零点问题，可令
，得
，然后在同一个坐标系中画出
和
的图像，通过观察图像，列式求解得
的取值范围．
因为是定义在
上的奇函数，所以的对称中心是
点，
因为
为偶函数，所以的对称轴是
，所以的对称轴是
，
所以的周期
，
且也是的对称轴，
因为是定义在上的奇函数，
时，
，
所以
时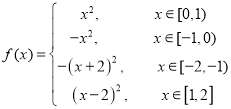
，
因为有三个零点，
所以令，得，
即和的图像有三个不同的交点，
因为在一个周期内，
当直线与在内相切时，令
，
得
，
，
所以
，得
，
此时，
在处得
，
即直线与在
内没有交点，在
内有两个交点，
所以要使和的图像有三个不同的交点，需
，
当直线与
在
内相切时，令
，
得
，
，
所以
，得
，
此时，
在
处得
，
即直线与在内没有交点，在内有两个交点，
所以要使和的图像有三个不同的交点，需
，
综上
，
所以，由周期性得
.
练习册系列答案
相关题目
