题目内容
若不等式|x-a|＜1的解集为{x|1＜x＜3}，则实数a的值为 ．
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：解绝对值不等式|x-a|＜1，可求得其解为a-1＜x＜a+1，依题意知，a-1=1且a+1=3，从而可得实数a的值．
解答：
解：∵|x-a|＜1，
∴-1＜x-a＜1，
∴a-1＜x＜a+1，
∴不等式|x-a|＜1的解集为{x|a-1＜x＜a+1}，
∵不等式|x-a|＜1的解集为{x|1＜x＜3}，
∴a-1=1且a+1=3，
解得：a=2．
故答案为：2．
∴-1＜x-a＜1，
∴a-1＜x＜a+1，
∴不等式|x-a|＜1的解集为{x|a-1＜x＜a+1}，
∵不等式|x-a|＜1的解集为{x|1＜x＜3}，
∴a-1=1且a+1=3，
解得：a=2．
故答案为：2．
点评：本题考查绝对值不等式的解法，考查等价转化思想与方程思想的应用，属于中档题．
练习册系列答案
应用题作业本系列答案
相关题目
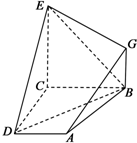如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=
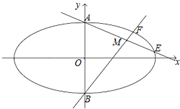已知椭圆Γ：