Question

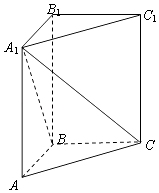
【题目】在如图所示的组合体中，三棱柱ABC﹣A1B1C1的侧面ABB1A1是圆柱的轴截面，C是圆柱底面圆周上不与A、B重合的一个点．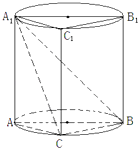
（Ⅰ）若圆柱的轴截面是正方形，当点C是弧AB的中点时，求异面直线A1C与AB1的所成角的大小；
（Ⅱ）当点C是弧AB的中点时，求四棱锥A1﹣BCC1B1与圆柱的体积比．

Answer 1

【答案】解：（Ⅰ）如图，取BC的中点D，连接OD，AD，则OD∥A1C，
∴∠AOD（或其补角）为异面直线A1C与AB1的所成角，
设正方形的边长为2，则△AOD中，OD= A1C= ，AO= ，AD= ，
∴cos∠AOD= =
∴∠AOD= ；
（Ⅱ）设圆柱的底面半径为r，母线长度为h，
当点C是弧AB的中点时， ，
， ，
∴ ．
【解析】（Ⅰ）取BC的中点D，连接OD，AD，则OD∥A1C，∠AOD（或其补角）为异面直线A1C与AB1的所成角，利用余弦定理，可求异面直线A1C与AB1的所成角的大小；（II）设圆柱的底面半径为r，母线长度为h，当点C是弧弧AB的中点时，求出三棱柱ABC﹣A1B1C1的体积，求出三棱锥A1﹣ABC的体积为，从而求出四棱锥A1﹣BCC1B1的体积，再求出圆柱的体积，即可求出四棱锥A1﹣BCC1B1与圆柱的体积比．
【考点精析】本题主要考查了旋转体（圆柱、圆锥、圆台）和异面直线及其所成的角的相关知识点，需要掌握常见的旋转体有：圆柱、圆锥、圆台、球；异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题．