题目内容
【题目】已知椭圆C1 ， 抛物线C2焦点均在x轴上，C1的中心和C2顶点均为原点O，从每条曲线上各取两个点，将其坐标记录于表中，则C1的左焦点到C2的准线之间的距离为（ ）
x | 3 | ﹣2 | 4 |
|
y | -2 | 0 | ﹣4 |
|
A.
-1
B.
-1
C.1
D.2
【答案】B
【解析】解：由表可知：抛物线C2焦点在x轴的正半轴，设抛物线C2：y2=2px（p＞0），则有 
=2p（x≠0），据此验证四个点知（3，﹣2 
），（4，﹣4）在C2上，代入求得2p=4，
∴抛物线C2的标准方程为y2=4x．则焦点坐标为（1，0），准线方程为：x=﹣1，
设椭圆C1： 
（a＞b＞0），把点（﹣2，0），（ 
， 
）代入得，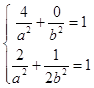 
，
解得：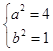 
，
∴C1的标准方程为 
+y2=1；
由c= 
= ，
左焦点（ ，0），
C1的左焦点到C2的准线之间的距离 ﹣1，
故选B．
练习册系列答案
相关题目
