��Ŀ����
����Ŀ�����һ�����дӵ�2����ÿһ������ǰһ��IJ����2������������Ϊ��H�����С���
��1��������{an}Ϊ��H�����С�����a1= ![]() ��3��a2=
��3��a2= ![]() ��a3=4����ʵ��m��ȡֵ��Χ��
��a3=4����ʵ��m��ȡֵ��Χ��
��2���Ƿ��������Ϊ1�ĵȲ�����{an}Ϊ��H�����С�������ǰn���Sn����Sn��n2+n��n��N*���������ڣ������{an}��ͨ�ʽ���������ڣ���˵�����ɣ�
��3����֪�ȱ�����{an}��ÿһ���Ϊ����������{an}Ϊ��H�����С���bn= ![]() an �� cn=
an �� cn= ![]() ��������{bn}���ǡ�H�����С�ʱ�����ж�����{cn}�Ƿ�Ϊ��H�����С�����˵�����ɣ�
��������{bn}���ǡ�H�����С�ʱ�����ж�����{cn}�Ƿ�Ϊ��H�����С�����˵�����ɣ�
���𰸡�
��1���⣺������ã�a2��a1=3��2��a3��a2=4�� ![]() ��2����2��
��2����2�� ![]() =
= ![]() ��0�����m
��0�����m ![]() ��m��0��
��m��0��
��ʵ��m��ȡֵ��Χʱ�����ޣ�0���� ![]()
��2���⣺������ڵȲ�����{an}Ϊ��H�����С����蹫��Ϊd����d��2����a1=1���ɵã�Sn=n+ ![]() ��������ɵã�n+
��������ɵã�n+ ![]() ��n2+n��n��N*����������d
��n2+n��n��N*����������d ![]() ����������
���������� ![]() =2+
=2+ ![]() ��2����
��2���� ![]()
![]() =2����d��2����d��2ì�ܣ���˲����ڵȲ�����{an}Ϊ��H�����С�
=2����d��2����d��2ì�ܣ���˲����ڵȲ�����{an}Ϊ��H�����С�
��3���⣺��ȱ�����{an}�Ĺ���Ϊq����an= ![]() ����ÿһ���Ϊ����������an+1��an=an��q��1����2��0��
����ÿһ���Ϊ����������an+1��an=an��q��1����2��0��
��a1��0��q��1����an+1��an=an��q��1����an��an��1����������{an��an��1}��n��2���У���a2��a1��Ϊ��С�
ͬ��������{bn��bn��1}��n��2���У���b2��b1��Ϊ��С���{an}Ϊ��H�����С�����ֻ֪��a2��a1��2��
�� a1��q��1����2������Ϊ{bn}���ǡ�H�����С����ҡ�b2��b1��Ϊ��С���b2��b1��2���� a1��q��1����3
��������{an}��ÿһ���Ϊ���������ɵ� a1��q��1��=3����a1=1��q=4��a1=3��q=2��
�ٵ�a1=1��q=4ʱ�� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]() ����
���� ![]()
= ![]() ��
��
��{dn}Ϊ�������У�
�� dn��dn��1��dn��2������d1��
�� cn+1��cn��cn��cn��1��cn��1��cn��2������c2��c1��
�� ![]() �����ԣ��������n��N*����cn+1��cn��2��
�����ԣ��������n��N*����cn+1��cn��2��
������{cn}Ϊ��H�����С����ڵ�a1=3��q=2ʱ�� ![]() ��
��
�� ![]() ����Ȼ��{cn}Ϊ�ݼ����У�c2��c1��0��2��
����Ȼ��{cn}Ϊ�ݼ����У�c2��c1��0��2��
������{cn}���ǡ�H�����С���
���ϣ��� ![]() ʱ������{cn}Ϊ��H�����С���
ʱ������{cn}Ϊ��H�����С���
�� ![]() ʱ������{cn}���ǡ�H�����С�
ʱ������{cn}���ǡ�H�����С�
����������1��������ã�a2��a1=3��2��a3��a2=4�� ![]() ��2����2��
��2����2�� ![]() =
= ![]() ��0�����m��Χ���ɵó�����2��������ڵȲ�����{an}Ϊ��H�����С����蹫��Ϊd����d��2����a1=1���ɵã�Sn=n+
��0�����m��Χ���ɵó�����2��������ڵȲ�����{an}Ϊ��H�����С����蹫��Ϊd����d��2����a1=1���ɵã�Sn=n+ ![]() ��������ɵã�n+
��������ɵã�n+ ![]() ��n2+n��n��N*����������d
��n2+n��n��N*����������d ![]() ����������������жϳ����ۣ���3����ȱ�����{an}�Ĺ���Ϊq����an=
����������������жϳ����ۣ���3����ȱ�����{an}�Ĺ���Ϊq����an= ![]() ����ÿһ���Ϊ����������an+1��an=an��q��1����2��0���ɵ�an+1��an=an��q��1����an��an��1 �� ��������{an��an��1}��n��2���У���a2��a1��Ϊ��С�ͬ��������{bn��bn��1}��n��2���У���b2��b1��Ϊ��С���{an}Ϊ��H�����С�����ֻ֪��a2��a1��2���� a1��q��1����2������Ϊ{bn}���ǡ�H�����С����ҡ�b2��b1��Ϊ��С��ɵ�b2��b1��2���� a1��q��1����3��������{an}��ÿһ���Ϊ���������ɵ� a1��q��1��=3��a1=1��q=4��a1=3��q=2��ͨ���������ۼ����жϳ����ۣ�
����ÿһ���Ϊ����������an+1��an=an��q��1����2��0���ɵ�an+1��an=an��q��1����an��an��1 �� ��������{an��an��1}��n��2���У���a2��a1��Ϊ��С�ͬ��������{bn��bn��1}��n��2���У���b2��b1��Ϊ��С���{an}Ϊ��H�����С�����ֻ֪��a2��a1��2���� a1��q��1����2������Ϊ{bn}���ǡ�H�����С����ҡ�b2��b1��Ϊ��С��ɵ�b2��b1��2���� a1��q��1����3��������{an}��ÿһ���Ϊ���������ɵ� a1��q��1��=3��a1=1��q=4��a1=3��q=2��ͨ���������ۼ����жϳ����ۣ�
�����㾫����������Ĺؼ������������е�ǰn��͵����֪ʶ����������{an}��ǰn���sn��ͨ��an�Ĺ�ϵ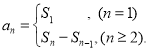 ��
��

 ��У����ϵ�д�
��У����ϵ�д�