题目内容
18．若复数z=（a-1）+3i（a∈R）在复平面内对应的点在直线y=x+2上，则a的值等于（ ）| A． | 1 | B． | 2 | C． | 5 | D． | 6 |
分析 求出对应点的坐标，代入直线方程，然后求解a的值．
解答 解：复数z=（a-1）+3i（a∈R）在复平面内对应的点在直线y=x+2上，
可得3=a-1+2，解得a=2．
故选：B．
点评 本题考查复数的几何意义，考查计算能力．
练习册系列答案
相关题目
9．如图，在平面四边形ABCD中，AB=1，$BC=\sqrt{3}+1$，$AD=\sqrt{6}$，∠ABC=120°，∠DAB=75°，则CD=（ ）
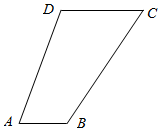
| A． | $\sqrt{3}$ | B． | $2\sqrt{2}$ | C． | $2\sqrt{3}$ | D． | $\sqrt{2}+1$ |
（文科）四棱镜P-ABCD中，PD⊥平面ABCD，2AD=AB=BC=2a，AD∥BC，PD=$\sqrt{3}$a，∠DAB=60°，Q是PB的中点．
如图，正方体ABCD-A1B1C1D1中，P是AD的中点．
在四棱锥P-ABCD中，平面四边形ABCD中AD∥BC，∠BAD为二面角B-PA-D一个平面角．
10．已知直线l：kx+y-2=0（k∈R）是圆C：x2+y2-6x+2y+9=0的对称轴，过点A（0，k）作圆C的一条切线，切点为B，则线段AB的长为（ ）
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 3 | D． | 2$\sqrt{3}$ |
8．已知函数f（x）=$\left\{\begin{array}{l}{{（\frac{1}{2}）}^{x}，x≤1}\\{{-x}^{2}+4x-\frac{5}{2}，x＞1}\end{array}\right.$ 函数g（x）=$\frac{3}{2}$x-a，其中a∈R，若函数y=f（x）-g（x）恰有3个零点，则a的取值范围是（ ）
| A． | （0，$\frac{15}{16}$） | B． | （$\frac{15}{16}$，1） | C． | （1，$\frac{16}{15}$） | D． | （1，$\frac{5}{4}$） |