题目内容
已知命题p：函数f（x）=
x3+x2+mx+1有两个不同的极值点；命题q：函数f（x）=x2-mx+3在区间[-1，2]是单调减函数．若p且￢q为真命题，求实数m的取值范围．
| 1 |
| 3 |
考点：复合命题的真假
专题：简易逻辑
分析：首先，判定命题p和命题q都为真命题时，实数m的取值范围，然后，结合条件p且￢q为真命题，进一步确定实数m的取值范围．
解答：
解：p为真时：f′（x）=x2+2x+m
△=4-4m＞0
∴m＜1
q为真时：m≥4
∴┐q为真时：m＜4
由
得：m＜1
∴实数m的取值范围为（-∞，1）．
△=4-4m＞0
∴m＜1
q为真时：m≥4
∴┐q为真时：m＜4
由
|
∴实数m的取值范围为（-∞，1）．
点评：本题重点考查了简单命题和复合命题的真假判断，属于中档题，准确理解复合命题的真假判断是解题关键．
练习册系列答案
相关题目
学校或班级举行活动，通常需要张贴海报进行宣传．现让你设计一张如图所示的竖向张贴的海报，要求版心面积为128dm2，上、下两边各空2dm，左、右两边各空1dm．如何设计海报的尺寸，才能使四周空白面积最小？
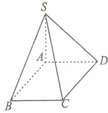如图，在四棱锥S-ABCD中，底面ABCD是菱形，SA⊥平面ABCD
