题目内容
1.已知正角α的终边上一点的坐标为($sin\frac{2π}{3},cos\frac{2π}{3}$),则角α的最小值为$\frac{11π}{6}$.分析 由题意可得角α为第四象限角,且tanα=-$\frac{\sqrt{3}}{3}$,由此可得角α的最小值.
解答 解:正角α的终边上一点的坐标为($sin\frac{2π}{3},cos\frac{2π}{3}$),即($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$),
则角α为第四象限角,且tanα=$\frac{y}{x}$=$\frac{-\frac{1}{2}}{\frac{\sqrt{3}}{2}}$=-$\frac{\sqrt{3}}{3}$,∴角α的最小值为2π-$\frac{π}{6}$=$\frac{11π}{6}$,
故答案为:$\frac{11π}{6}$.
点评 本题主要考查任意角的三角函数的定义,诱导公式,属于基础题.

练习册系列答案
相关题目
12.30岁以后,随着年龄的增长,人们的身体机能在逐渐退化,所以打针 买保健品这样的“健康消费”会越来越多,现对某地区不同年龄段的一些人进行了调查,得到其一年内平均“健康消费”如表:
(1)求“健康消费”y关于年龄x的线性回归方程;
(2)由(1)所得方程,估计该地区的人在60岁时的平均“健康消费”.
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 |
| 健康消费(百元) | 5 | 8 | 10 | 14 | 18 |
(2)由(1)所得方程,估计该地区的人在60岁时的平均“健康消费”.
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)
9.设实数x,y满足不等式组$\left\{\begin{array}{l}x+2y-5≥0\\ 2x+y-4≤0\\ x-y+3≥0\end{array}\right.$,则x+y的最小值是( )
| A. | 3 | B. | -3 | C. | $\frac{7}{3}$ | D. | -$\frac{7}{3}$ |
10.已知集合M={0,1,2,3,4},N={2,4,6},P=M∩N,则P的子集有( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
11.已知点P为不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.$所表示的平面区域内的一点,点Q是M:(x+1)2+y2=1上的一个动点,则当∠MPQ最大时,|PQ|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{11}}}{3}$ | D. | $\frac{{2\sqrt{5}}}{3}$ |
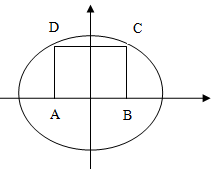 如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.
如图,长为2$\sqrt{3}$,宽为$\frac{1}{2}$的矩形ABCD,以A、B为焦点的椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1恰好过C、D两点.