题目内容
设直角三角形的两条直角边的长分别为a,b,斜边长为c,斜边上的高为h,则有:
①a2+b2>c2+h2;
②a3+b3<c3+h3;
③a4+b4>c4+h4;
④a5+b5<c5+h5.
其中正确结论的序号是 .
①a2+b2>c2+h2;
②a3+b3<c3+h3;
③a4+b4>c4+h4;
④a5+b5<c5+h5.
其中正确结论的序号是
考点:余弦定理
专题:解三角形
分析:由题意可得ab=ch,可得h=
.a2+b2=c2.令
=cosθ,
=sinθ,θ∈(0,
).利用三角函数的单调性即可得出.
| ab |
| c |
| a |
| c |
| b |
| c |
| π |
| 2 |
解答:
解:由题意可得ab=ch,可得h=
.a2+b2=c2.
令
=cosθ,
=sinθ,θ∈(0,
).
①左边=a2+b2=c2<c2+h2=右边,不正确;
②a3+b3<c3+h3,化为cos3θ+sin3θ<1+(
)3.
由cos3θ+sin3θ<cos2θ+sin2θ=1<1+(
)3.
因此正确.
由此可得:③不正确;④正确.
其中正确结论的序号是②④.
| ab |
| c |
令
| a |
| c |
| b |
| c |
| π |
| 2 |
①左边=a2+b2=c2<c2+h2=右边,不正确;
②a3+b3<c3+h3,化为cos3θ+sin3θ<1+(
| h |
| c |
由cos3θ+sin3θ<cos2θ+sin2θ=1<1+(
| h |
| c |
因此正确.
由此可得:③不正确;④正确.
其中正确结论的序号是②④.
点评:本题考查了勾股定理、三角函数的单调性、三角形的面积计算公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=cos2x-tcosx在x∈[
,
]上为单调递增函数,则实数t的取值范围是( )
| π |
| 6 |
| π |
| 3 |
A、[2
| ||
B、[
| ||
| C、(-∞,2] | ||
| D、(-∞,1] |
 如图是一个边长为4的正方形及扇形(见阴影部分),若随机向正方形内丢一粒豆子,则豆子落入扇形的概率是( )
如图是一个边长为4的正方形及扇形(见阴影部分),若随机向正方形内丢一粒豆子,则豆子落入扇形的概率是( )A、
| ||
B、
| ||
C、
| ||
| D、π |
斜率不存在的直线一定是( )
| A、平行于x轴的直线 |
| B、垂直于x轴的直线 |
| C、垂直于y轴的直线 |
| D、垂直于坐标轴的直线 |
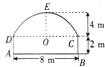 如图所示的图形为一隧道的截面,其中ABCD是矩形,CED是抛物线的一段,在工程的设计中,要注意开凿隧道所需挖掘的土石方量,这就需要计算这个截面的面积,试根据图中所给出的数据计算这个截面的面积.
如图所示的图形为一隧道的截面,其中ABCD是矩形,CED是抛物线的一段,在工程的设计中,要注意开凿隧道所需挖掘的土石方量,这就需要计算这个截面的面积,试根据图中所给出的数据计算这个截面的面积.