题目内容
8. 如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点
如图,正方体的棱长为a,P、Q分别为A1D、B1D1的中点(1)求证:PQ∥平面AA1B1B
(2)求PQ的长.
分析 (1)以D1为原点,D1A1为x轴,D1C1为y轴,D1D为z轴,建立空间直角坐标系,利用向量法能证明PQ∥平面AA1B1B.
(2)由已知条件利用向量法能求出PQ的长.
解答 证明:(1)以D1为原点,D1A1为x轴,D1C1为y轴,D1D为z轴,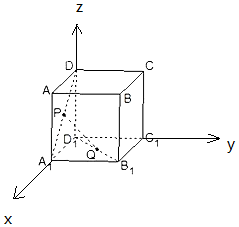
建立空间直角坐标系,
P($\frac{a}{2}$,0,$\frac{a}{2}$),Q($\frac{a}{2},\frac{a}{2}$,0),
$\overrightarrow{PQ}$=(0,$\frac{a}{2}$,-$\frac{a}{2}$),
平面AA1B1B的法向量$\overrightarrow{n}$=(1,0,0),
∵$\overrightarrow{PQ}•\overrightarrow{n}$=0,PQ?平面AA1B1B,
∴PQ∥平面AA1B1B.
解:(2)PQ的长|$\overrightarrow{PQ}$|=$\sqrt{(\frac{a}{2})^{2}+(-\frac{a}{2})^{2}}$=$\frac{\sqrt{2}}{2}a$.
点评 本题考查线面平行的证明,考查线段长的求法,考查推理论证能力、运算求解能力、空间思维能力、空间想象能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
6.化简sin690°的值是( )
| A. | 0.5 | B. | -0.5 | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
7.已知三条不重合的直线m,n,l 和两个不重合的平面 α,β 下列命题正确的是( )
| A. | 若m∥n,n?α,则 m∥α | B. | 若α⊥β,α∩β=m,m⊥n,则 n⊥α | ||
| C. | 若l⊥n,m⊥n,则 l∥m | D. | 若l⊥α,m⊥β,且 l⊥m,则 α⊥β |
16.若一个圆柱的正视图与其侧面展开图是相似矩形,则这个圆柱的全面积与侧面积之比为( )
| A. | $1+\sqrt{π}$ | B. | 1+$\frac{1}{{\sqrt{π}}}$ | C. | $1+\frac{1}{{\sqrt{2π}}}$ | D. | $1+\frac{1}{{2\sqrt{π}}}$ |
17.下列结论正确的是( )
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | “若am2<bm2,则a<b”的逆命题为真命题 | |
| D. | 若${(\sqrt{x}-\frac{1}{{2\root{3}{x}}})^n}$的展开式中第四项为常数项,则n=5 |
18.户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下联表:已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是$\frac{3}{5}$
(1)请将列联表补充完整:
(2)是否有99%的把握认为喜欢户外运动与性别有关?并说明理由.下面临界值仅供参考:(大于2.706-90%,大于3.841-95%,大于6.635-99%)
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜欢户外活动 | 不喜欢户外活动 | 合计 | |
| 男性 | 20 | 5 | 25 |
| 女性 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(2)是否有99%的把握认为喜欢户外运动与性别有关?并说明理由.下面临界值仅供参考:(大于2.706-90%,大于3.841-95%,大于6.635-99%)
(参考公式:K2=$\frac{{n(ad-bc)}^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)