题目内容
11.已知函数f(x)=x2-2x+3的定义域为[0,3],则函数f(x)的值域为[2,6].分析 配方得到f(x)=(x-1)2+2,而f(x)的定义域为[0,3],这样便可求出f(x)的最大值和最小值,从而求出f(x)的值域.
解答 解:f(x)=(x-1)2+2;
∵x∈[0,3];
∴x=1时,f(x)取最小值2;x=3时,f(x)取最大值6;
∴f(x)的值域为[2,6].
故答案为:[2,6].
点评 考查函数定义域、值域的概念,以及配方求二次函数值域的方法.

练习册系列答案
相关题目
1.已知数列{an}为的等差数列,且a1+a7+a13=3,则a7的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
19.执行如图所示的程序框图,如果是输入的变量t∈[-2,-1],则输出的S属于( )
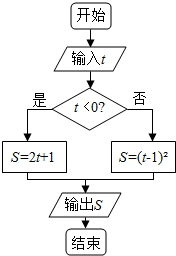

| A. | (-5,-3) | B. | [-3,-1] | C. | [4,9] | D. | [-3,4] |
6.已知a=log0.50.9,b=log0.50.8,c=0.5-0.9,则( )
| A. | b<a<c | B. | a<b<c | C. | c<b<a | D. | c<a<b |

 设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-a,x<1}\\{{x}^{2}-4ax+3{a}^{2},x≥1}\end{array}\right.$
设函数f(x)=$\left\{\begin{array}{l}{{3}^{x}-a,x<1}\\{{x}^{2}-4ax+3{a}^{2},x≥1}\end{array}\right.$