题目内容
15.(1)函数$y=ln(x-2)+\sqrt{3-x}$的定义域(2,3].(2)方程${2^{2x-1}}=\frac{1}{4}$的解x=$\frac{1}{2}$.
分析 (1)由$\left\{\begin{array}{l}{x-2>0}\\{3-x≥0}\end{array}\right.$,可得2<x≤3,即可求出函数$y=ln(x-2)+\sqrt{3-x}$的定义域;
(2)方程可化为22x-1=2-2,即可得出结论.
解答 解:(1)由$\left\{\begin{array}{l}{x-2>0}\\{3-x≥0}\end{array}\right.$,可得2<x≤3,
∴函数$y=ln(x-2)+\sqrt{3-x}$的定义域为(2,3];
(2)方程可化为22x-1=2-2,∴2x-1=-2,∴x=$\frac{1}{2}$.
故答案为:(2,3];$\frac{1}{2}$.
点评 本题考查函数的定义域,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
12.函数f(x)=sin(2x+$\frac{π}{3}$)-$\frac{1}{2016}$(0≤x≤$\frac{4π}{3}$)的零点为x1,x2,x3(x1<x2<x3),则$\frac{cos({x}_{1}+{x}_{2})}{sin({x}_{2}+{x}_{3})}$=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | -$\frac{\sqrt{3}}{3}$ |
10.图中的几何体是下列图中的( )绕线旋转一周得到的.


| A. |  | B. |  | C. |  | D. |  |
7.如图是一个程序框图,则输出的n的值是 ( )
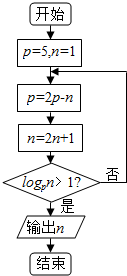

| A. | 29 | B. | 31 | C. | 61 | D. | 63 |