题目内容
2．执行如图所示的程序框图，当输入n=100时，试写出其输出S的数学式子（不要求写出运算结果）．
分析 执行程序框图，依次写出每次循环得到的S，i的值，当i=101＞100，退出循环，输出S的值，即可得解．
解答 解：第一次执行：S=0+12，i=2；
第二次执行：S=12+22，i=3；
第三次执行：S=12+22+32，i=4； …（5分）
…
当i=100时，满足i≤n，S=12+22+32+…+1002，i=101；
i=101不满足条件，退出循环，输出S．
所以，S=12+22+32+…+1002．…（10分）
点评 本题主要考察了程序框图和算法，正确理解循环结构的功能是解题的关键，属于基本知识的考查．
练习册系列答案
相关题目
12．执行如图所示的程序框图，输出的S值为（ ）
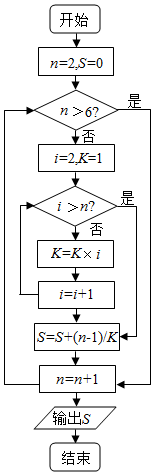
| A． | $\frac{119}{120}$ | B． | $\frac{359}{360}$ | C． | $\frac{719}{720}$ | D． | $\frac{5039}{5040}$ |
13．
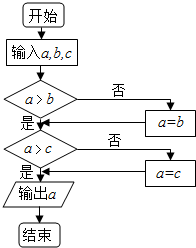已知：a，b，c为集合A={1，2，3，4，5}中三个不同的数，通过如框图给出的一个算法输出一个整数a，则输出的数a=4的概率是（ ）
已知：a，b，c为集合A={1，2，3，4，5}中三个不同的数，通过如框图给出的一个算法输出一个整数a，则输出的数a=4的概率是（ ）| A． | $\frac{3}{8}$ | B． | $\frac{3}{20}$ | C． | $\frac{3}{10}$ | D． | $\frac{1}{2}$ |
10．“x为无理数”是“x2为无理数”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
17．篮球运动员乙在某几场比赛中得分的茎叶图如图所示，则他在这几场比赛中得分的中位数为（ ）
| A． | 26 | B． | 27 | C． | 26.5 | D． | 27.5 |
7．设 a=${（\frac{1}{3}）^{0.2}}，b={2^{\frac{1}{3}}}$，则a，b 的大小关系是（ ）
| A． | a＞b | B． | a＜b | C． | a=b | D． | 不能确定 |
14．复数z=（-2-i）i在复平面内对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
12．函数f（x）=sin（2x+$\frac{π}{3}$）-$\frac{1}{2016}$（0≤x≤$\frac{4π}{3}$）的零点为x1，x2，x3（x1＜x2＜x3），则$\frac{cos（{x}_{1}+{x}_{2}）}{sin（{x}_{2}+{x}_{3}）}$=（ ）
| A． | $\sqrt{3}$ | B． | -$\sqrt{3}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | -$\frac{\sqrt{3}}{3}$ |