题目内容
2.已知不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$,构成平面区域Ω(其中x,y是变量),则目标函数z=3x+6y的最小值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
分析 作出不等式组表示的平面区域Ω,变形目标函数并平移直线y=$-\frac{1}{2}$x可得结论.
解答  解:作出不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$表示的平面区域Ω(如图阴影部分所示),
解:作出不等式组$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-3≤0}\\{y≥0}\end{array}\right.$表示的平面区域Ω(如图阴影部分所示),
变形目标函数可得y=$-\frac{1}{2}$x+$\frac{1}{6}$z,平移直线y=$-\frac{1}{2}$x可知,
当直线经过点C(-2,0)时,直线的截距最小,z取最小值-6
故选:C.
点评 本题考查简单线性规划,数形结合是解决问题的关键,属中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
10.下列集合中与集合{x|x=2k+1,k∈N+}不相等的是( )
| A. | {x|x=2k-1,k∈N+} | B. | {x|x=4k±1,k∈N+} | ||
| C. | {x|x=2k-1,k∈N且k>1} | D. | {x|x=2k+3,k∈N} |
17.数列{an}满足a1=1,对任意的n∈N*都有an+1=a1+an+n,则$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{{{a_{2016}}}}$=( )
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{4032}{2017}$ | D. | $\frac{4034}{2017}$ |
7.已知A(-1,1)、B(x-1,2x),若向量$\overrightarrow{OA}$与$\overrightarrow{OB}$(O为坐标原点)的夹角为锐角,则实数x的取值范围是( )
| A. | (-1,$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) | B. | (-1,+∞) | C. | (-1,3)∪(3,+∞) | D. | (-∞,-1) |
14.若△ABC的面积S△ABC∈[$\frac{\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$],且$\overrightarrow{AB}$•$\overrightarrow{BC}$=3,则向量$\overrightarrow{BA}$与$\overrightarrow{BC}$夹角的取值范围是( )
| A. | [$\frac{π}{3}$,$\frac{π}{2}$] | B. | [$\frac{3π}{4}$,$\frac{5π}{6}$] | C. | [$\frac{2π}{3}$,π) | D. | [$\frac{2π}{3}$,$\frac{5π}{6}$] |
12.抛物线x2=2y上的点到直线x-2y-4=0的距离的最小值是( )
| A. | $\frac{\sqrt{5}}{4}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{3\sqrt{5}}{4}$ | D. | $\frac{3\sqrt{5}}{5}$ |
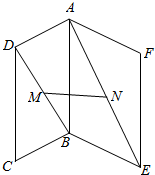 如图,边长相等的两个正方形ABCD和ABEF所在平面相交于AB,M∈BD,N∈AE且BM=EN≠BD.求证:MN⊥AB.
如图,边长相等的两个正方形ABCD和ABEF所在平面相交于AB,M∈BD,N∈AE且BM=EN≠BD.求证:MN⊥AB.