题目内容
已知函数f(x)=ax2+1,g(x)=ln(x+1)
(Ⅰ)实数a为何值时,函数g(x)在x=0处的切线与函数f(x)的图象也相切;
(Ⅱ)当x∈[0,+∞)时,都有不等式f(x)+g(x)≤x+1成立,求a的取值范围;
(Ⅲ)已知n∈N,试判断g(n)与g′(0)+g′(1)+g′(2)+…+g′(n+1)的大小,并证明之.
(Ⅰ)实数a为何值时,函数g(x)在x=0处的切线与函数f(x)的图象也相切;
(Ⅱ)当x∈[0,+∞)时,都有不等式f(x)+g(x)≤x+1成立,求a的取值范围;
(Ⅲ)已知n∈N,试判断g(n)与g′(0)+g′(1)+g′(2)+…+g′(n+1)的大小,并证明之.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:分类讨论,导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(Ⅰ)求出g(x)的导数,求得切点斜率和切点,得到切线方程,联立f(x),消去y,运用判别式为0,即可解得a;
(Ⅱ)不等式f(x)+g(x)≤x+1成立,即为ax2+ln(1+x)-x≤0在x≥0时恒成立,令h(x)=ax2+ln(1+x)-x,求出h(x)的导数,对a讨论,当a≤0时,当a>0时判断单调性,进而得到a的范围;
(Ⅲ)g(n)<g′(0)+g′(1)+g′(2)+…+g′(n+1).令l(x)=g(x)-x=ln(1+x)-x,(x>0),求出导数判断在x>0的单调性,再令x=
,k=1,2,3,…,n.并累加,运用对数的运算性质,即可得证.
(Ⅱ)不等式f(x)+g(x)≤x+1成立,即为ax2+ln(1+x)-x≤0在x≥0时恒成立,令h(x)=ax2+ln(1+x)-x,求出h(x)的导数,对a讨论,当a≤0时,当a>0时判断单调性,进而得到a的范围;
(Ⅲ)g(n)<g′(0)+g′(1)+g′(2)+…+g′(n+1).令l(x)=g(x)-x=ln(1+x)-x,(x>0),求出导数判断在x>0的单调性,再令x=
| 1 |
| k |
解答:
解:(Ⅰ)g(x)=ln(x+1)的导数为g′(x)=
,
则函数g(x)在x=0处的切线斜率为1,
又切点为(0,0),
即有切线方程为y=x,
联立y=ax2+1,消去y,得ax2-x+1=0,
a=0时,y=f(x)=1,显然不相切.
即有a≠0,△=0,即1-4a=0,解得a=
,
则有a=
时,函数g(x)在x=0处的切线与函数f(x)的图象也相切;
(Ⅱ)不等式f(x)+g(x)≤x+1成立,即为
ax2+ln(1+x)-x≤0在x≥0时恒成立,
令h(x)=ax2+ln(1+x)-x,h′(x)=2ax+
-1=
=2ax-1,
当a≤0,x≥0时,h′(x)<0,h(x)在[0,+∞)递减,
即有h(x)≤h(0),即为ax2+ln(1+x)-x≤0成立;
当a>0时,x>
时,h′(x)>0,h(x)递增,
0<x<
时,h′(x)<0,h(x)递减.
即有x=
,h(x)取得极小值,也为最小值,
则ax2+ln(1+x)-x≤0在x≥0时不恒成立.
综上可得,a的取值范围是(-∞,0];
(Ⅲ)g(n)<g′(0)+g′(1)+g′(2)+…+g′(n+1).
理由如下:令l(x)=g(x)-x=ln(1+x)-x,(x>0),
l′(x)=
-1=
,由x>0,则l′(x)<0,l(x)递减,
l(x)<l(0)=0,
即有ln(1+x)<x,
令x=
,k=1,2,3,…,n.并累加可得,
ln2+ln
+ln
+…+ln
<1+
+
+…+
,
即有ln(2•
•
•…•
)<1+
+
+…+
,
即ln(n+1)<1+
+
+…+
,
由
+
>0,
即有1+
+
+…+
+
+
>ln(n+1).
故g(n)<g′(0)+g′(1)+g′(2)+…+g′(n+1).
| 1 |
| 1+x |
则函数g(x)在x=0处的切线斜率为1,
又切点为(0,0),
即有切线方程为y=x,
联立y=ax2+1,消去y,得ax2-x+1=0,
a=0时,y=f(x)=1,显然不相切.
即有a≠0,△=0,即1-4a=0,解得a=
| 1 |
| 4 |
则有a=
| 1 |
| 4 |
(Ⅱ)不等式f(x)+g(x)≤x+1成立,即为
ax2+ln(1+x)-x≤0在x≥0时恒成立,
令h(x)=ax2+ln(1+x)-x,h′(x)=2ax+
| 1 |
| 1+x |
| 2ax2+(2a-1)x-1 |
| 1+x |
=2ax-1,
当a≤0,x≥0时,h′(x)<0,h(x)在[0,+∞)递减,
即有h(x)≤h(0),即为ax2+ln(1+x)-x≤0成立;
当a>0时,x>
| 1 |
| 2a |
0<x<
| 1 |
| 2a |
即有x=
| 1 |
| 2a |
则ax2+ln(1+x)-x≤0在x≥0时不恒成立.
综上可得,a的取值范围是(-∞,0];
(Ⅲ)g(n)<g′(0)+g′(1)+g′(2)+…+g′(n+1).
理由如下:令l(x)=g(x)-x=ln(1+x)-x,(x>0),
l′(x)=
| 1 |
| 1+x |
| -x |
| 1+x |
l(x)<l(0)=0,
即有ln(1+x)<x,
令x=
| 1 |
| k |
ln2+ln
| 3 |
| 2 |
| 4 |
| 3 |
| n+1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
即有ln(2•
| 3 |
| 2 |
| 4 |
| 3 |
| n+1 |
| n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
即ln(n+1)<1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
由
| 1 |
| n+1 |
| 1 |
| n+2 |
即有1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
故g(n)<g′(0)+g′(1)+g′(2)+…+g′(n+1).
点评:本题考查导数的运用:求切线方程和判断单调性,主要考查单调性的运用:求最值和证明不等式,运用分类讨论的思想方法是解题的关键,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
设集合A,B,C满足:A∪∁RB=A∪∁RC,则下列( )必成立.
| A、B=C |
| B、A∩B=A∩C |
| C、∁RA∩B=∁RA∩C |
| D、A∩∁RB=A∩∁RC |
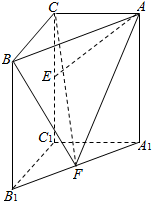 如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
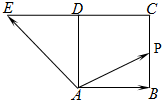 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若动点P从点A出发,沿正方形的边按如下路线运动:A→B→C→D→E→A→D,其中
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若动点P从点A出发,沿正方形的边按如下路线运动:A→B→C→D→E→A→D,其中