题目内容
4.若2sin2x-5sin2y=1,求cos2x+siny的取值范围$[-\frac{\sqrt{5}}{5},\frac{3}{5}]$.分析 2sin2x-5sin2y=1,可得:cos2x=$\frac{1-5si{n}^{2}y}{2}$≥0,解得$-\frac{\sqrt{5}}{5}$≤siny≤$\frac{\sqrt{5}}{5}$.cos2x+siny=$-\frac{5}{2}$$(siny-\frac{1}{5})^{2}$+$\frac{3}{5}$,再利用二次函数的单调性即可得出.
解答 解:∵2sin2x-5sin2y=1,
∴2(1-cos2x)-5sin2y=1,
解得cos2x=$\frac{1-5si{n}^{2}y}{2}$≥0,解得0≤sin2y$≤\frac{1}{5}$,∴$-\frac{\sqrt{5}}{5}$≤siny≤$\frac{\sqrt{5}}{5}$.
∴cos2x+siny
=$\frac{1-5si{n}^{2}y}{2}$+siny
=$-\frac{5}{2}$$(siny-\frac{1}{5})^{2}$+$\frac{3}{5}$,
∵$-\frac{\sqrt{5}}{5}$≤siny≤$\frac{\sqrt{5}}{5}$,
当siny=$\frac{1}{5}$时,cos2x+siny取得最大值$\frac{3}{5}$.
当siny=-$\frac{\sqrt{5}}{5}$时,cos2x+siny取得最小值$-\frac{\sqrt{5}}{5}$.
∴cos2x+siny∈$[-\frac{\sqrt{5}}{5},\frac{3}{5}]$,
故答案为:$[-\frac{\sqrt{5}}{5},\frac{3}{5}]$.
点评 本题考查了三角函数的单调性与值域、二次函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
14.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$夹角为45°,且|$\overrightarrow{a}$|=2,|$\overrightarrow{a}$-$\overrightarrow{b}$|=2.则|$\overrightarrow{b}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
12.现代产品的销售离不开广告的促销活动,某公司代理一种国际品牌智能环境检测设备,其广告费用x(单位:万元)与年销售量t(单位:件)的统计数据如表所示:
这里所给出的数据表示t对x呈线性回归关系$\stackrel{∧}{t}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
[参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$].
(1)根据所给数据求出线性回归方程;
(2)将(1)中的$\stackrel{∧}{t}$近似地看作产品的实际年销售量t,若该产品的销售单价g(x)(单位:万元)与广告费x的近似关系是g(x)=$\left\{\begin{array}{l}{17-2x(x∈{N}^{*},且1≤x≤5)}\\{6-\frac{2}{x}(x∈{N}^{*},且6≤x≤10)}\end{array}\right.$试问当公司投入广告费用多少万元时,公司每年获得的销售收入最大,最大销售收入是多少万元?
| 广告费用x(万元) | 3 | 4 | 5 | 6 |
| 年销售量t(件) | 25 | 30 | 40 | 45 |
[参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$].
(1)根据所给数据求出线性回归方程;
(2)将(1)中的$\stackrel{∧}{t}$近似地看作产品的实际年销售量t,若该产品的销售单价g(x)(单位:万元)与广告费x的近似关系是g(x)=$\left\{\begin{array}{l}{17-2x(x∈{N}^{*},且1≤x≤5)}\\{6-\frac{2}{x}(x∈{N}^{*},且6≤x≤10)}\end{array}\right.$试问当公司投入广告费用多少万元时,公司每年获得的销售收入最大,最大销售收入是多少万元?
16.点P在直径为2的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
| A. | $\frac{2\sqrt{70}}{5}$ | B. | $\frac{3\sqrt{70}}{5}$ | C. | $\frac{4\sqrt{15}}{5}$ | D. | $\frac{6\sqrt{15}}{5}$ |
14.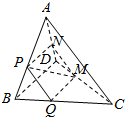 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
 如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )
如图,在四面体ABCD中,截面PQMN是正方形,且PQ∥AC,则下列命题中,错误的是( )| A. | AC⊥BD | B. | AC∥截面PQMN | ||
| C. | AC=BD | D. | 异面直线PM与BD所成的角为45° |
 已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\sqrt{2}$,一条准线方程为x=$\frac{\sqrt{2}}{2}$,直线l与双曲线右支及双曲线的渐近线交于A、B、C、D四点,四个点的顺序如图所示.
已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\sqrt{2}$,一条准线方程为x=$\frac{\sqrt{2}}{2}$,直线l与双曲线右支及双曲线的渐近线交于A、B、C、D四点,四个点的顺序如图所示.