题目内容
9.在△ABC中,角A,B,C的对边分别为a,b,c.已知,A+3C=π.(1)若$\frac{b}{c}$=$\sqrt{3}$,求角C;
(2)若△ABC为锐角三角形,求cosB取值范围.
分析 (1)利用三角形内角和定理与正弦定理、倍角公式即可得出.
(2)由于△ABC为锐角三角形,B=2C∈$(0,\frac{π}{2})$,A=π-3C=$π-\frac{3}{2}B$∈$(0,\frac{π}{2})$,解出即可得出.
解答 解:(1)∵A+3C=π=A+B+C,∴B=2C.
∵$\frac{b}{c}$=$\sqrt{3}$,∴$\frac{sinB}{sinC}$=$\sqrt{3}$=$\frac{sin2C}{sinC}$=2cosC,
∴cosC=$\frac{\sqrt{3}}{2}$,又C∈(0,π),
∴$C=\frac{π}{6}$.
(2)∵△ABC为锐角三角形,B=2C∈$(0,\frac{π}{2})$,
A=π-3C=$π-\frac{3}{2}B$∈$(0,\frac{π}{2})$,
解得$\frac{π}{3}$<B$<\frac{π}{2}$,
∴cosB∈$(0,\frac{1}{2})$.
点评 本题考查了三角形内角和定理、正弦定理、锐角三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
20.已知函数f(x)=$\left\{\begin{array}{l}{kx+2,x≥0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$,则下列关于函数y=f[f(x)]-$\frac{3}{2}$的零点个数的判断正确的是( )
| A. | 当k≥0时,有1个零点;当k<0时,有2个零点 | |
| B. | 当k≥0时,没有零点;当-$\frac{1}{2}$<k≤-$\frac{1}{4}$时,有3个零点,当k≤-$\frac{1}{2}$或-$\frac{1}{4}$<k<0有2个零点 | |
| C. | 当k≥0时,没有零点;当-$\frac{1}{2}$<k<0时,有3个零点,当k≤-$\frac{1}{2}$有2个零点 | |
| D. | 当k≥0时,没有零点;当-$\frac{1}{2}$≤k<-$\frac{1}{4}$时,有3个零点,当k<-$\frac{1}{2}$或-$\frac{1}{4}$≤k<0有2个零点 |
14.一个三角形在一个平面上的投影是( )
| A. | 一个三角形 | B. | 一条线段 | ||
| C. | 一个点 | D. | 一个三角形或一条线段 |
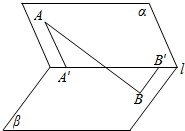 如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.
如图,二面角a-l-β为60°,A∈a,B∈β,AA′⊥l交l于A′,BB′⊥l交1于B′,若AA′=2,BB′=1,A′B′=$\sqrt{3}$.