题目内容
 已知函数fn(x)=x3-nx-1(x>0),n∈N*.
已知函数fn(x)=x3-nx-1(x>0),n∈N*.(Ⅰ)求函数f3(x)的极值;
(Ⅱ)判断函数fn(x)在区间(
| n |
| n+1 |
(Ⅲ)阅读右边的程序框图,请结合试题背景简要描述其算法功能,并求出执行框图所表达的算法后输出的n值.
考点:利用导数研究函数的极值,程序框图
专题:计算题,函数的性质及应用,导数的综合应用,算法和程序框图
分析:(Ⅰ)写出f3(x),求出导数,令导数大于0,小于0,得到单调区间,从而得到极小值;
(Ⅱ)函数fn(x)在区间(
,
)上有且只有一个零点.运用零点存在定理,说明存在一个零点,再判断fn(x)在区间(
,
)上单调递增,即可得证;
(Ⅲ)程序框图的算法功能:找出最小的正整数n,使fn(x)的零点an满足
≥an.
根据fn(x)在区间(
,
)上单调递增,判断当n≤3时,
<an;当n≥4时,
>an.即可得到答案.
(Ⅱ)函数fn(x)在区间(
| n |
| n+1 |
| n |
| n+1 |
(Ⅲ)程序框图的算法功能:找出最小的正整数n,使fn(x)的零点an满足
| ||||
| 2 |
根据fn(x)在区间(
| n |
| n+1 |
| ||||
| 2 |
| ||||
| 2 |
解答:
解:(Ⅰ)∵f3(x)=x3-3x-1,∴f3′(x)=3x2-3,
∵当x>1时,f3′(x)>0,函数递增;当0<x<1时,f3′(x)<0,函数递减.
∴当x=1时,f3(x)取得唯一的一个极小值-3,无极大值;
(Ⅱ)函数fn(x)在区间(
,
)上有且只有一个零点.
证明如下:∵fn(
)=(
)3-n
-1=-1<0,fn(
)=(
)3-n
-1=
-1>0,fn(
)•fn(
)<0,
∴函数fn(x)在区间(
,
)上必定存在零点.
∵fn′(x)=3x2-n,∴当x∈(
,
)时,fn′(x)>3(
)2-n=2n>0,
∴fn(x)在区间(
,
)上单调递增,
∴函数fn(x)在区间(
,
)上的零点最多一个.
综上知:函数fn(x)在区间(
,
)上存在唯一零点;
(Ⅲ)程序框图的算法功能:找出最小的正整数n,使fn(x)的零点an满足
≥an.
∵fn(
)=(
)3-n•
-1=
-1,
∴当0<n≤3时,fn(
)<0=fn(an);
当n≥4时,fn(
)>0=fn(an).
又∵fn(x)在区间(
,
)上单调递增,
∴当n≤3时,
<an;当n≥4时,
>an.
∴输出的n值为4.
∵当x>1时,f3′(x)>0,函数递增;当0<x<1时,f3′(x)<0,函数递减.
∴当x=1时,f3(x)取得唯一的一个极小值-3,无极大值;
(Ⅱ)函数fn(x)在区间(
| n |
| n+1 |
证明如下:∵fn(
| n |
| n |
| n |
| n+1 |
| n+1 |
| n+1 |
| n+1 |
| n |
| n+1 |
∴函数fn(x)在区间(
| n |
| n+1 |
∵fn′(x)=3x2-n,∴当x∈(
| n |
| n+1 |
| n |
∴fn(x)在区间(
| n |
| n+1 |
∴函数fn(x)在区间(
| n |
| n+1 |
综上知:函数fn(x)在区间(
| n |
| n+1 |
(Ⅲ)程序框图的算法功能:找出最小的正整数n,使fn(x)的零点an满足
| ||||
| 2 |
∵fn(
| ||||
| 2 |
| ||||
| 2 |
| ||||
| 2 |
3
| ||||
| 8 |
∴当0<n≤3时,fn(
| ||||
| 2 |
当n≥4时,fn(
| ||||
| 2 |
又∵fn(x)在区间(
| n |
| n+1 |
∴当n≤3时,
| ||||
| 2 |
| ||||
| 2 |
∴输出的n值为4.
点评:本题主要考查函数、导数、零点、算法初步等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程
=0.68
+54.6,利用下表中数据推断a的值为( )
| ? |
| y |
| ? |
| x |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 | a | 75 | 81 | 89 |
| A、68.2 | B、68 |
| C、69 | D、67 |
一组数据中每个数据都减去50构成一组新数据,则这组新数据的平均数是1.2,方差是4.4,则原来一组数的方差为( )
| A、3.2 | B、4.4 |
| C、4.8 | D、5.6 |
 如图所示,已知A1B1C1-ABC是三棱柱,E、E1分别是AC、A1C1的中点.求证:平面AB1E1∥平面BEC1.
如图所示,已知A1B1C1-ABC是三棱柱,E、E1分别是AC、A1C1的中点.求证:平面AB1E1∥平面BEC1.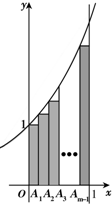 如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于
如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于