题目内容
8.已知曲线C的极坐标方程是ρ-8cosθ+4sinθ+$\frac{4}{ρ}$=0,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,在平面直角坐标系xOy中,直线l经过点P(5,-2),倾斜角α=$\frac{π}{3}$.(1)学出曲线C的直角坐标方程和直线l的参数方程;
(2)设l与曲线C相交于A,B两点,求|AB|的值.
分析 (1)曲线C的极坐标方程是ρ-8cosθ+4sinθ+$\frac{4}{ρ}$=0,即ρ2-8ρcosθ+4ρsinθ+4=0,利用互化公式可得直角坐标方程.由直线l经过点P(5,-2),倾斜角α=$\frac{π}{3}$.可得参数方程:$\left\{\begin{array}{l}{x=5+\frac{1}{2}t}\\{y=-2+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数).
(2)直线l的普通方程:y=$\sqrt{3}$x-2-5$\sqrt{3}$.圆C的方程配方为:(x-4)2+(y+2)2=16,可得圆心C(4,-2),半径r=4.求出圆心C到直线l的距离d,利用弦长公式即可得出.
解答 解:(1)曲线C的极坐标方程是ρ-8cosθ+4sinθ+$\frac{4}{ρ}$=0,即ρ2-8ρcosθ+4ρsinθ+4=0,
可得直角坐标方程:x2+y2-8x+4y+4=0,
由直线l经过点P(5,-2),倾斜角α=$\frac{π}{3}$.可得参数方程:$\left\{\begin{array}{l}{x=5+\frac{1}{2}t}\\{y=-2+\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数).
(2)直线l的普通方程:y=$\sqrt{3}$x-2-5$\sqrt{3}$.
x2+y2-8x+4y+4=0,配方为:(x-4)2+(y+2)2=16,可得圆心C(4,-2),半径r=4.
∴圆心C到直线l的距离d=$\frac{|4\sqrt{3}-2+2-5\sqrt{3}|}{2}$=$\frac{\sqrt{3}}{2}$.
∴|AB|=2$\sqrt{{4}^{2}-(\frac{\sqrt{3}}{2})^{2}}$=$\sqrt{61}$.
点评 本题考查了极坐标方程化为直角坐标方程、直线的参数方程、勾股定理与弦长公式,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $-\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{π}{3}$ |
 某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )
某几何体的三视图如图所示(在右边的网格线中,每个小正方形的边长为1),则该几何体的表面积为( )| A. | 48 | B. | 54 | C. | 60 | D. | 64 |
 如图所示,若输出的S为1525,则判断框内应填( )
如图所示,若输出的S为1525,则判断框内应填( )| A. | k<4 | B. | k≤4 | C. | k>4 | D. | k≥4 |
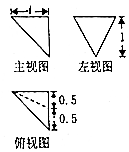
| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
| A. | A${\;}_{27-n}^{8}$ | B. | A${\;}_{34-n}^{27-n}$ | C. | A${\;}_{34-n}^{7}$ | D. | A${\;}_{34-n}^{8}$ |