题目内容
经过抛物线y2=4x的焦点且垂直于直线3x-2y=0的直线l的方程是（ ）
| A、3x-2y-3=0 |
| B、6x-4y-3=0 |
| C、2x+3y-2=0 |
| D、2x+3y-1=0 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设出垂线方程，求出焦点坐标，然后求解即可．
解答：
解：设垂直于直线3x-2y=0的直线l的方程为2x+3y+c=0，
由于直线l经过抛物线y2=4x的焦点为F（1，0），
所以c=-2．
故选C．
由于直线l经过抛物线y2=4x的焦点为F（1，0），
所以c=-2．
故选C．
点评：本题考查抛物线的基本性质，直线方程的应用，考查计算能力．
练习册系列答案
相关题目
已知经过点p（m，-4）可以引圆x2+y2-2x+4y+8=m2+2m的两条切线，则实数m的取值范围是（ ）
| A、m＞2或m＜-3 |
| B、m＜2 |
| C、1＜m＜2 |
| D、1＜m＜2或m＜-3 |
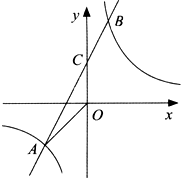如图，已知A（n，-2），B（1，4）是一次函数y=kx+b的图象和反比例函数y=