题目内容
在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,
且AC=AD=CD=DE=2,AB=1.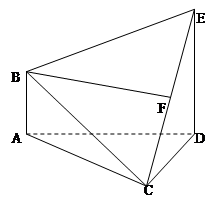
(Ⅰ)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(Ⅱ)求多面体ABCDE的体积.
(1)F为线段CE的中点 (2)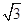
解析试题分析:(Ⅰ)由已知AB⊥平面ACD,DE⊥平面ACD,∴AB//ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则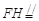
 ,∴
,∴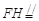
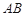 ,
,
∴四边形ABFH是平行四边形,∴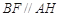 ,
,
由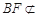 平面ACD内,
平面ACD内,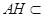 平面ACD,
平面ACD,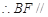 平面ACD;
平面ACD;
(Ⅱ)取AD中点G,连接CG..
AB 平面ACD, ∴CG
平面ACD, ∴CG AB
AB
又CG AD ∴CG
AD ∴CG 平面ABED, 即CG为四棱锥的高, CG=
平面ABED, 即CG为四棱锥的高, CG=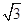
∴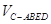 =
=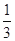
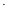
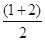
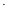 2
2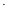
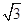 =
=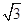 .
.
考点:线面平行和多面体的体积
点评:主要是考查了线面平行以及多面体体积的运算,属于中档题。

练习册系列答案
相关题目
 中,四边形
中,四边形 是边长为
是边长为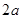 的正方形,平面
的正方形,平面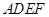 垂直于平面
垂直于平面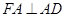 ,
,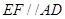 ,
,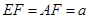 .
.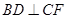 ;
;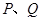 分别为棱
分别为棱 和
和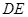 的中点,求证:
的中点,求证: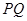 ∥平面
∥平面
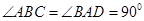 ,
,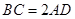 ,
, 和
和 都是等边三角形.
都是等边三角形.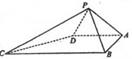
 ;
; 中,
中, ,
,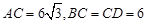 ,设顶点
,设顶点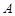 在底面
在底面 上的射影为
上的射影为 .
.
 ;
;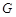 在棱
在棱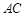 上,且
上,且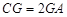 ,试求二面角
,试求二面角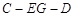 的余弦值.
的余弦值. 是⊙
是⊙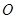 的直径,
的直径,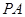 垂直于⊙
垂直于⊙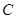 是圆周上不同于
是圆周上不同于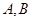 的任意一点,(1) 求证:
的任意一点,(1) 求证: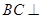 平面
平面 。(2) 求二面角 P-BC-A 的大小。
。(2) 求二面角 P-BC-A 的大小。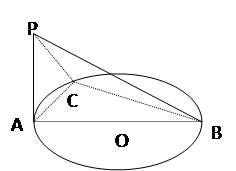
 ⊥平面
⊥平面 ,
,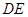 ∥
∥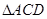 是正三角形,
是正三角形,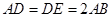 ,且
,且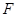 是
是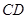 的中点.
的中点.
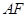 ∥平面
∥平面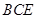 ;
; .
.
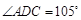 ,
,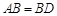 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD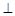 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.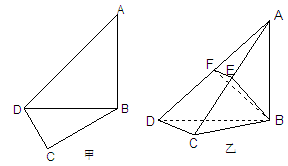
 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
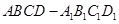 ,
,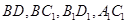 分别为各个面的对角线;
分别为各个面的对角线;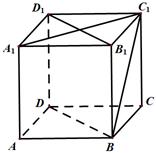
 ;
;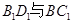 所成的角.
所成的角.