题目内容
如图,在三棱锥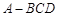 中,
中,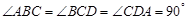 ,
,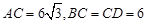 ,设顶点
,设顶点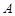 在底面
在底面 上的射影为
上的射影为 .
.
(Ⅰ)求证: ;
;
(Ⅱ)设点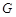 在棱
在棱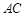 上,且
上,且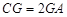 ,试求二面角
,试求二面角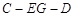 的余弦值.
的余弦值.
(1)根据题意,由于已知条件可知 平面
平面 ,那么利用线面垂直的性质定理得到。
,那么利用线面垂直的性质定理得到。
(2)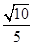
解析试题分析:证明:(I)方法一:由 平面
平面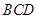 得
得
 ,
,
又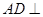
 ,则
,则 平面
平面 ,
,
故 , 2分
, 2分
同理可得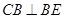 ,则
,则 为矩形,又
为矩形,又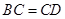 ,
,
则 为正方形,故
为正方形,故 . 4分
. 4分
方法二:由已知可得 ,设
,设 为
为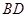 的中点,则
的中点,则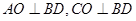 ,则
,则 平面
平面 ,故平面
,故平面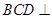 平面
平面 ,则顶点
,则顶点 在底面
在底面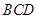 上的射影
上的射影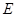 必在
必在 ,故
,故 .
.
(II)方法一:由(I)的证明过程知 平面
平面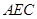 ,过
,过 作
作 ,垂足为
,垂足为 ,则易证得
,则易证得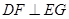 ,故
,故 即为二面角
即为二面角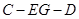 的平面角, 7分
的平面角, 7分
由已知可得 ,则
,则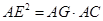 ,故
,故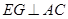 ,则
,则 ,
,
又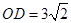 ,则
,则 , 9分
, 9分
故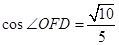 ,即二面角
,即二面角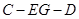 的余弦值为
的余弦值为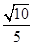 . 11分
. 11分
方法二: 由(I)的证明过程知 为正方形,如图建立坐标系,
为正方形,如图建立坐标系,
则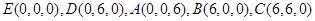 ,
,
可得 , 7分
, 7分
则 ,易知平面
,易知平面
的一个法向量为 ,设平面
,设平面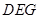 的一个法向量为
的一个法向量为 ,则由
,则由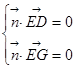 得
得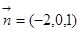 , 9分
, 9分
则 ,即二面角
,即二面角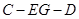 的余弦值为
的余弦值为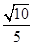 . 11分
. 11分
考点:线面垂直的性质定理以及二面角的大小
点评:主要是考查了线面垂直以及二面角的平面角的求解的运用属于基础题。

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 所在的平面与正方形
所在的平面与正方形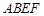 所在的平面相互垂直,
所在的平面相互垂直,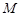 、
、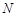 分别是
分别是 、
、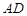 的中点.
的中点.
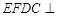 面
面 ;
; 与平面
与平面 所成的角正弦值.
所成的角正弦值.



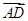 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);
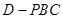 的体积.
的体积.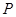 为平行四边形
为平行四边形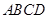 所在平面外一点,
所在平面外一点,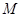 为
为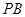 的中点,
的中点,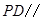 平面
平面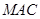 .
.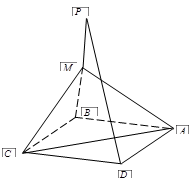

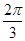 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.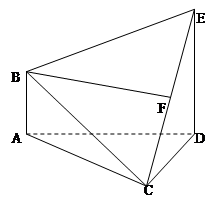
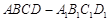 中,
中,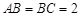 ,过
,过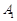 、
、 、
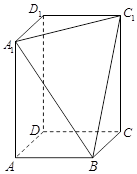
、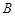 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体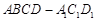 ,且这个几何体的体积为
,且这个几何体的体积为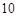 .
.
 的长;
的长;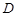 到平面
到平面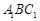 的距离.
的距离.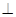 平面EFDC.
平面EFDC.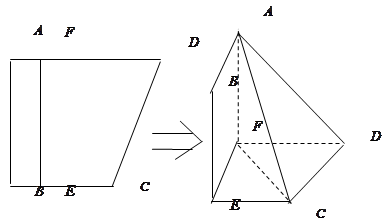
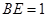 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点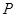 ,且
,且 ,使得CP∥平面ABEF?若存在,求出
,使得CP∥平面ABEF?若存在,求出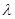 的值;若不存在,说明理由;
的值;若不存在,说明理由;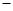 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.