题目内容
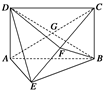
如图甲,在平面四边形ABCD中,已知
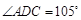 ,
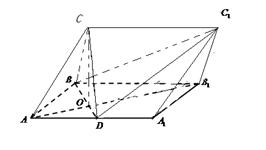
,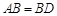 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.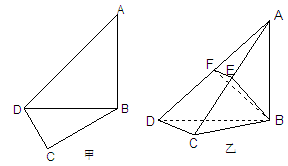
(Ⅰ)求证:DC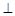 平面ABC;
平面ABC;
(Ⅱ)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
(1)对于线面垂直的证明,一般先证明线线垂直,然后根据DC⊥BC,以及AB⊥CD.来得到。
(2)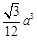
解析试题分析:(Ⅰ)证明:在图甲中∵ 且
且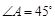 ∴
∴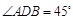 ,
,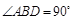
即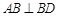
在图乙中,∵平面ABD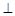 平面BDC , 且平面ABD
平面BDC , 且平面ABD 平面BDC=BD
平面BDC=BD
∴AB⊥底面BDC,∴AB⊥CD.
又 ,∴DC⊥BC,且
,∴DC⊥BC,且
∴DC 平面ABC.
平面ABC.
(Ⅱ)解:∵E、F分别为AC、AD的中点
∴EF//CD,又由(Ⅰ)知,DC 平面ABC,
平面ABC,
∴EF⊥平面ABC,
∴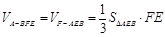
在图甲中,∵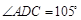 , ∴
, ∴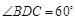 ,
,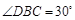
由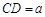 得
得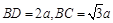 ,
,
∴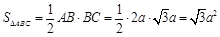 ∴
∴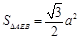
∴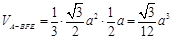 .
.
考点:线面垂直,和几何体体积
点评:主要是考查了空间中线面垂直的证明,以及三棱锥的体积的求解,属于基础题。

练习册系列答案
相关题目
 中,
中,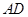 ⊥平面
⊥平面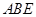 ,
,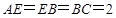 ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面 .
.
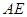 ⊥平面
⊥平面 ;
;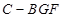 的体积.
的体积.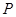 为平行四边形
为平行四边形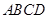 所在平面外一点,
所在平面外一点,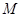 为
为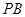 的中点,
的中点,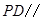 平面
平面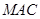 .
.
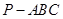 ,底面
,底面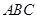 为边长为
为边长为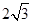 的正三角形,平面
的正三角形,平面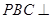 平面
平面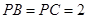 ,
,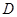 为
为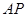 上一点,
上一点,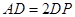 ,
,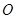 为底面三角形中心.
为底面三角形中心. 
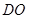 ∥面
∥面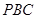 ;
;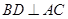 ;
;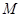 为
为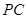 中点,求二面角
中点,求二面角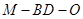 的余弦值.
的余弦值.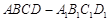 中,
中,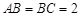 ,过
,过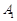 、
、 、
、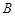 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体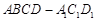 ,且这个几何体的体积为
,且这个几何体的体积为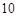 .
.
 的长;
的长; 到平面
到平面 的距离.
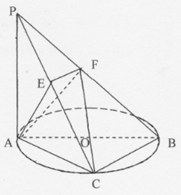
的距离.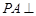 ⊙
⊙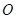 所在的平面,
所在的平面,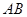 是⊙
是⊙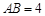 ,C是⊙
,C是⊙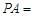
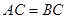 ,
,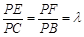 .
.
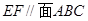 ;
;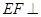
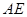 ;
;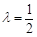 时,求三棱锥
时,求三棱锥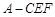 的体积.
的体积.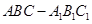 中,四边形
中,四边形 是正方形,
是正方形,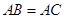 ,
, ,
,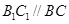 且
且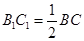 ,二面角
,二面角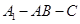 是直二面角
是直二面角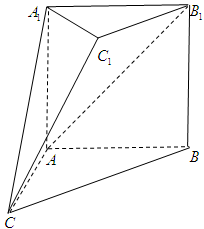
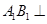 平面
平面 ;
; 平面
平面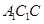 。
。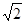 ,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.
,D为AA1中点,BD与AB1交于点O,CO丄侧面ABB1A1.