题目内容
18．设命题p：函数f（x）=x2+2x+m的图象与x轴没有交点；命题q：m2-2m-3＜0．若“p∨q”为真，“p∧q”为假．求实数m的取值范围．分析 若“p∨q”为真，“p∧q”为假．则p，q一真一假，进而可得实数m的取值范围．
解答 解：当命题p为真命题时：△=4-4m＜0，
解得：m＞1
当命题q为真命题时：-1＜m＜3，
若“p∨q”为真，“p∧q”为假．则p，q一真一假，
当p真q假时，m≥3，
当p假q真时，-1＜m≤1，
综上可得：实数m的取值范围为：m≥3或-1＜m≤1．
点评 本题以命题的真假判断与应用为载体，考查了复合命题，函数的图象，二次不等式的解法等知识点，难度中档．
练习册系列答案
相关题目
已知an=2n-1（n∈N*），把数列{an}的各项排成如图所示的三角形数阵，记S（m，n）表示该数阵中第m行中从左到右的第n个数，则S（8，6）=（ ）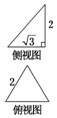
已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一条直角边为2的直角三角形，则该三棱锥的正视图可能为（ ）
