题目内容
已知函数f(x)=cos(ωx-
)(ω>0)满足f(x+π)+f(x)=0,则函数g(x)=sin(
-ωx)的单调递增区间为( )
| π |
| 6 |
| π |
| 6 |
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
考点:正弦函数的单调性,余弦函数的单调性
专题:三角函数的求值,三角函数的图像与性质
分析:求出函数的周期,然后求出ω,利用正弦函数的单调区间求解即可.
解答:
解:因为函数f(x)=cos(ωx-
)(ω>0)满足f(x+π)=-f(x),
所以最小正周期为2π,所以
=2π,解得ω=1.
所以g(x)=sin(
-x)=-sin(x-
).
由
+2kπ≤x-
≤
+2kπ,k∈Z,得
+2kπ≤x≤
+2kπ,k∈Z.
故选:D.
| π |
| 6 |
所以最小正周期为2π,所以
| 2π |
| ω |
所以g(x)=sin(
| π |
| 6 |
| π |
| 6 |
由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| 2π |
| 3 |
| 5π |
| 3 |
故选:D.
点评:本题考查三角函数的单调性的求法,函数的周期的应用,考查计算能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知扇形的弧长是4cm,半径是2cm2,则扇形的圆心角的弧度数是( )
| A、2 | B、1 | C、4 | D、3 |
 已知程序如图所示.
已知程序如图所示.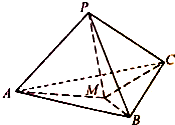 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(